题目内容
在下列区间中,是函数y=sin(x+
)的一个递增区间的是( )
| π |
| 4 |
A、[
| ||||
B、[0,
| ||||
| C、[-π,0] | ||||
D、[
|
考点:正弦函数的单调性
专题:计算题,三角函数的图像与性质
分析:利用正弦函数的单调性,可求得函数y=sin(x+
)的递增区间,再对k赋值,利用集合间的包含关系判断即可.
| π |
| 4 |
解答:
解:由2kπ-
≤x+
≤2kπ+
(k∈Z)得:2kπ-
≤x≤2kπ+
(k∈Z),
∴函数y=sin(x+
)的递增区间为[2kπ-
,2kπ+
](k∈Z),
当k=0时,[-
,
]为函数y=sin(x+
)的一个递增区间,
又[0,
]?[-
,
],
∴区间[0,
]为函数y=sin(x+
)的一个递增区间.
故选:B.
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
∴函数y=sin(x+
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
当k=0时,[-
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
又[0,
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
∴区间[0,
| π |
| 4 |
| π |
| 4 |
故选:B.
点评:本题考查正弦函数的单调性,考查集合间的包含关系,属于中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
空间直角坐标系中,已知A(1,-2,1),B(2,2,2),点P在z轴上,且满足|PA|=|PB|,则P点的坐标为
( )
( )
| A、(3,0,0) |
| B、(0,3,0) |
| C、(0,0,3) |
| D、(0,0,-3) |
7个人站一队,其中甲在排头,乙不在排尾,则不同的排列方法有( )
| A、720 | B、600 |
| C、576 | D、324 |
某三棱锥的三视图如图所示,该三棱锥的体积为( )


| A、2 | B、3 | C、4 | D、6 |
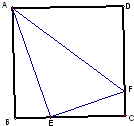 如图,△AEF是边长为x的正方形ABCD的内接三角形,已知∠AEF=90°,AE=a,EF=b,a>b,则x=
如图,△AEF是边长为x的正方形ABCD的内接三角形,已知∠AEF=90°,AE=a,EF=b,a>b,则x=