题目内容
①f(x)=
,g(x)=x
②f(x)=
,g(x)=
③f(x)=x,g(x)=
④f(x)=|x+1|,g(x)=
上述四组函数,表示同一函数的是 .
| x2 |
②f(x)=
| x2-4 |
| x+2 |
| x-2 |
③f(x)=x,g(x)=
| x2 |
| x |
④f(x)=|x+1|,g(x)=
|
上述四组函数,表示同一函数的是
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:根据所给函数的定义域、对应关系判定函数是否为同一函数即可.
解答:
解:①f(x)=
=|x|,g(x)=x,对应关系不同,不是同一函数;
②f(x)=
的定义域是(-∞,-2]∪[2,+∞),g(x)的定义域是[2,+∞),定义域不同,不是同一函数;
③f(x)=x的定义域是R,g(x)=
的定义域是(-∞,0)∪(0,+∞),定义域不同,不是同一函数;
④f(x)=|x+1|=
,与g(x)的定义域相同,对应关系也相同,∴是同一函数;
故答案为:④.
| x2 |
②f(x)=
| x2-4 |
③f(x)=x的定义域是R,g(x)=
| x2 |
| x |
④f(x)=|x+1|=
|
故答案为:④.
点评:本题考查了根据函数的定义域、对应关系判定函数是否为同一函数的问题,是基础题.

练习册系列答案
相关题目
空间直角坐标系中,已知A(1,-2,1),B(2,2,2),点P在z轴上,且满足|PA|=|PB|,则P点的坐标为
( )
( )
| A、(3,0,0) |
| B、(0,3,0) |
| C、(0,0,3) |
| D、(0,0,-3) |
某三棱锥的三视图如图所示,该三棱锥的体积为( )


| A、2 | B、3 | C、4 | D、6 |
如果球的大圆周长为C,则这个球的表面积是( )
A、
| ||
B、
| ||
C、
| ||
| D、2πC2 |
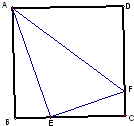 如图,△AEF是边长为x的正方形ABCD的内接三角形,已知∠AEF=90°,AE=a,EF=b,a>b,则x=
如图,△AEF是边长为x的正方形ABCD的内接三角形,已知∠AEF=90°,AE=a,EF=b,a>b,则x=