题目内容
当a<0时,关于x的不等式(x-5a)(x+a)>0的解集是 .
考点:其他不等式的解法
专题:不等式的解法及应用
分析:当a<0时,则有5a<-a,由关于x的不等式(x-5a)(x+a)>0,可得 x<5a,或x>-a,从而求得不等式的解集.
解答:
解:当a<0时,则有5a<-a,
根据关于x的不等式(x-5a)(x+a)>0,
可得 x<5a,或x>-a,
故答案为:{x|x<5a,或x>-a}.
根据关于x的不等式(x-5a)(x+a)>0,
可得 x<5a,或x>-a,
故答案为:{x|x<5a,或x>-a}.
点评:本题主要考查一元二次不等式的解法,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
空间直角坐标系中,已知A(1,-2,1),B(2,2,2),点P在z轴上,且满足|PA|=|PB|,则P点的坐标为
( )
( )
| A、(3,0,0) |
| B、(0,3,0) |
| C、(0,0,3) |
| D、(0,0,-3) |
双曲线
-
=1(a>0,b>0)的离心率的取值范围正好是函数f(x)=2x+2-x(-1≤x≤2)的值域,则该双曲线渐近线的斜率取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||||||||||||
B、[
| ||||||||||||
C、[-
| ||||||||||||
D、[-
|
 一正棱柱其三视图如图所示,该正多面体的体积为
一正棱柱其三视图如图所示,该正多面体的体积为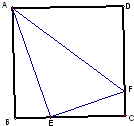 如图,△AEF是边长为x的正方形ABCD的内接三角形,已知∠AEF=90°,AE=a,EF=b,a>b,则x=
如图,△AEF是边长为x的正方形ABCD的内接三角形,已知∠AEF=90°,AE=a,EF=b,a>b,则x=