题目内容
在△ABC中,角A、B.C的对边分别是a、b、c,B=
.
(Ⅰ)若a=2,b=
,求△ABC的面积;
(Ⅱ)若A>
,求
的取值范围.
| π |
| 3 |
(Ⅰ)若a=2,b=
| 3 |
(Ⅱ)若A>
| π |
| 2 |
| a |
| c |
考点:正弦定理
专题:解三角形
分析:(Ⅰ)利用余弦定理获得关于c的方程求得c,进而利用三角形面积公式求得三角形的面积.
(Ⅱ)通过正弦定理表示出
,通过C的范围确定其范围.
(Ⅱ)通过正弦定理表示出
| a |
| c |
解答:
解:(Ⅰ)∵b2=a2+c2-2accosB,
∴3=4+c2-2c=0,即c2-2c+1=0,
∴c=1,
∴S=
acsinB=
×2×
=
.
(Ⅱ)
=
=
=
+
,
∵A=
-C>
,
∴0<C<
,
∴0<tanC<
,
∴
+
>
×
+
=2,即
>2.
∴3=4+c2-2c=0,即c2-2c+1=0,
∴c=1,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
(Ⅱ)
| a |
| c |
| sinA |
| sinC |
sin(
| ||
| sinC |
| ||
| 2tanC |
| 1 |
| 2 |
∵A=
| 2π |
| 3 |
| π |
| 2 |
∴0<C<
| π |
| 6 |
∴0<tanC<
| π |
| 3 |
∴
| ||
| 2tanC |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| a |
| c |
点评:本题主要查了正弦定理和余弦定理的综合运用.在解三角形问题中的范围问题,一定要注意题设中隐含的角的范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在四边形ABCD中,“
=2
”是“四边形ABCD为梯形”的( )
| AB |
| DC |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在△ABC中,边a,b,c所对的角分别为A,B,C,若a=
,b=
,B=60°,则A=( )
| 2 |
| 3 |
| A、135° | B、45° |
| C、135°或45° | D、90° |
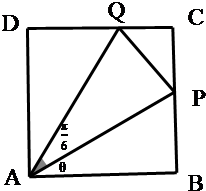 如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=
如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=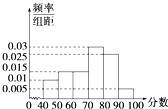 某校举行了由全部学生参加的校园安全知识考试,从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100]后,画出如图所示的频率分布直方图.观察图形的信息,回答下列问题:估计这次考试的及格率(60分及以上为及格)为
某校举行了由全部学生参加的校园安全知识考试,从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100]后,画出如图所示的频率分布直方图.观察图形的信息,回答下列问题:估计这次考试的及格率(60分及以上为及格)为