题目内容
13.已知函数f(x)=2sinxcosx+1-2cos2(x-$\frac{π}{12}$),(x∈R),则下列结论正确的是( )| A. | 周期T=2π | B. | f(x)向左平移$\frac{π}{6}$后是奇函数 | ||
| C. | 一个对称中心是($\frac{π}{3}$,0) | D. | 一条对称轴是x=$\frac{π}{6}$ |
分析 先利用二倍角公式和三函数恒等式求出f(x)=sin(2x-$\frac{π}{3}$),由此利用正弦函数性质能求出结果.
解答 解:∵f(x)=2sinxcosx+1-2cos2(x-$\frac{π}{12}$),(x∈R),
∴f(x)=sin2x-cos(2x-$\frac{π}{6}$)
=sin2x-(cos2xcos$\frac{π}{6}$+sin2xsin$\frac{π}{6}$)
=$\frac{1}{2}sin2x$-$\frac{\sqrt{3}}{2}cos2x$
=sin(2x-$\frac{π}{3}$),
∴f(x)的周期T=$\frac{2π}{2}$=π,故A错误;
f(x)向左平移$\frac{π}{6}$后,得到y=$sin[2(x+\frac{π}{6})-\frac{π}{3}]=sin2x$,是奇函数,故B正确;
f(x)的对称中心($\frac{kπ}{2}+\frac{5π}{6}$,0),k∈Z,故C错误;
f(x)的对称轴方程为x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,故D错误.
故选:B.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意二倍角公式、三函数恒等式和三角函数性质的合理运用.

练习册系列答案
相关题目
4.当m=7时,执行如图所示的程序框图,输出的S值为( )
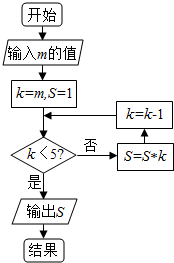

| A. | 7 | B. | 42 | C. | 210 | D. | 840 |
8.已知集合U=R,A={y|y=x2+x},B={y|y=($\frac{1}{2}$)x},则∁UB)∩A=( )
| A. | [-$\frac{1}{4}$,0] | B. | (0,$\frac{1}{4}$] | C. | (-∞,$\frac{1}{4}$] | D. | [$\frac{1}{4}$,1) |
18.若a+bi=$\frac{5}{1+2i}$(i是虚数单位,a,b∈R),则ab=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
5.若函数f(x)=exsinx,则此函数图象在点(4,f(4))处的切线的倾斜角为( )
| A. | 钝角 | B. | 0 | C. | $\frac{π}{2}$ | D. | 锐角 |
3.满足A⊆{1,2,3,4},且A∩{2,3,4}={ 3,4}的集合A的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |