题目内容

4．当m=7时，执行如图所示的程序框图，输出的S值为（　　）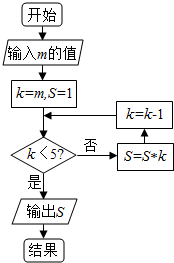
A．7B．42C．210D．840

分析 该算法的功能是求S=7×6×…×k的值，根据条件确定跳出循环的k值，即可得出输出S的值．

解答 解：由程序框图知：该算法的功能是求S=7×6×…×k的值，
当m=7时，k=5-1=4，
即跳出循环的k值为4，
∴输出的S=7×6×5=210．
故选：C．

点评 本题考查了循环结构的程序框图，根据框图的流程判断算法的功能是解答本题的关键．

练习册系列答案
相关题目
14．定义在实数集R上的函数f（x），如果存在函数g（x）=Ax+B（A，B为常数），使得f（x）≥g（x）对一切实数x都成立，那么称g（x）为函数f（x）的一个承托函数．下列说法正确的有：①③．（写出所有正确说法的序号）
①对给定的函数f（x），对承托函数可能不存在，也可能有无数个；
②定义域和值域都是R的函数f（x），不存在承托函数；
③g（x）=ex为函数f（x）=ex的一个承托函数；
④函数f（x）=$\frac{x}{{x}^{2}+x+1}$不存在承托函数．
15．已知函数f（x）=sinxcos2$\frac{α}{2}$+$\frac{1}{2}$cosxsinα-$\frac{1}{2}$sinx（0＜α＜π）在x=π时有最小值-$\frac{1}{2}$．
（1）求α的值；
（2）在△ABC中，a，b，c分别是角A，B，C所对的边，已知a=1，b=$\sqrt{3}$，f（A）=$\frac{\sqrt{3}}{4}$，求角C的值．
12．一个几何体的三视图如图所示，则这个几何体外接球的体积为（　　）
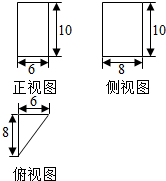
A．1000$\sqrt{2}$πB．200πC．$\frac{200}{3}$πD．$\frac{1000\sqrt{2}}{3}$π
19．已知$sinθ-cosθ=-\frac{1}{5}$
（1）求sinθcosθ的值．
（2）求sin3θ-cos3θ的值．
（3）当-π＜θ＜0时，求tanθ的值．
9．已知函数f（x）=sinx+cosx，则下列结论正确的是（　　）
A．函数f（x）的图象关于直线$x=-\frac{π}{4}$对称B．函数f（x）的最大值为2
C．函数f（x）在区间$（-\frac{π}{4}，\frac{π}{4}）$上是增函数D．函数f（x）的最小正周期为π
16．cos40°sin20°+sin140°cos20°=（　　）
A．$\frac{1}{2}$B．$\frac{{\sqrt{3}}}{2}$C．$-\frac{1}{2}$D．$-\frac{{\sqrt{3}}}{2}$
13．已知函数f（x）=2sinxcosx+1-2cos2（x-$\frac{π}{12}$），（x∈R），则下列结论正确的是（　　）
A．周期T=2πB．f（x）向左平移$\frac{π}{6}$后是奇函数
C．一个对称中心是（$\frac{π}{3}$，0）D．一条对称轴是x=$\frac{π}{6}$
14．在△ABC中，内角A，B，C的对边分别为a，b，c．已知$cosA=\frac{2}{3}，sinB=\sqrt{5}cosC$．
（1）求tanC的值；
（2）若$a=\sqrt{2}$，求边c的长及△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网