题目内容
3.曲线f(x)=$\sqrt{x}$+$\frac{4}{x}$+1在(1,6)处的切线经过过点A(-1,y1),B(3,y2),则y1与y2的等差中项为( )| A. | -6 | B. | -4 | C. | 4 | D. | 6 |
分析 由导数的几何意义求出曲线f(x)=$\sqrt{x}$+$\frac{4}{x}$+1在(1,6)处的切线为y=-$\frac{7}{2}x+\frac{19}{2}$,由此求出y1,y2,从而能求出y1与y2的等差中项.
解答 解:∵f(x)=$\sqrt{x}$+$\frac{4}{x}$+1,∴${f}^{'}(x)=\frac{1}{2\sqrt{x}}-\frac{4}{{x}^{2}}$,
∴f′(1)=$\frac{1}{2}-4$=-$\frac{7}{2}$,
∴曲线f(x)=$\sqrt{x}$+$\frac{4}{x}$+1在(1,6)处的切线为:y-6=-$\frac{7}{2}(x-1)$,即y=-$\frac{7}{2}x+\frac{19}{2}$,
∵切线经过过点A(-1,y1),B(3,y2),
∴${y}_{1}=\frac{7}{2}+\frac{19}{2}=13$,${y}_{2}=-\frac{7}{2}×3+\frac{19}{2}$=-1,
∴y1与y2的等差中项:
A=$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{13-1}{2}$=6.
故选:D.
点评 本题考查等差中项的求法,是中档题,解题时要认真审题,注意导数的几何意义的合理运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4.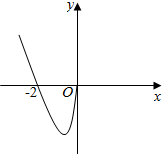 已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )
已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )
 已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )
已知函数f(x)满足对任意x∈R都有f(x)+f(-x)=0,且在(-∞,0]上的图象如图所示,则关于x的不等式$\frac{f(x)-f(-x)}{x}$<0的解集为( )| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(2,+∞) | C. | (-2,2) | D. | (-∞,-2)∪(0,2) |
11.已知命题p:对任意x∈R,总有|x|≥0;命题q:x=2是方程x+2=0的根.则下列命题为真命题的是( )
| A. | p∧¬q | B. | ¬p∧q | C. | ¬p∧¬q | D. | p∧q |
12.一个几何体的三视图如图所示,则这个几何体外接球的体积为( )
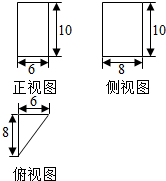

| A. | 1000$\sqrt{2}$π | B. | 200π | C. | $\frac{200}{3}$π | D. | $\frac{1000\sqrt{2}}{3}$π |
13.已知函数f(x)=2sinxcosx+1-2cos2(x-$\frac{π}{12}$),(x∈R),则下列结论正确的是( )
| A. | 周期T=2π | B. | f(x)向左平移$\frac{π}{6}$后是奇函数 | ||
| C. | 一个对称中心是($\frac{π}{3}$,0) | D. | 一条对称轴是x=$\frac{π}{6}$ |