题目内容
1.已知在△ABC中,角A、B、C所对应的边为a,b,c.(I)若sin(A+$\frac{π}{3}$)=$\frac{2\sqrt{3}}{3}$cosA,求A的值;
(Ⅱ)若cosA=$\frac{1}{3}$,b=3c,求sinC的值.
分析 (I)利用两角和的正弦函数公式,特殊角的三角函数值,同角三角函数基本关系式化简已知可得:tanA=$\frac{\sqrt{3}}{3}$,结合范围A∈(0,π),即可解得A的值.
(Ⅱ)利用同角三角函数基本关系式可求sinA,利用余弦定理可求a=$2\sqrt{2}$c,利用正弦定理即可求得sinC的值.
解答 解:(I)∵sin(A+$\frac{π}{3}$)=$\frac{2\sqrt{3}}{3}$cosA,
∴$\frac{1}{2}$sinA+$\frac{\sqrt{3}}{2}$cosA=$\frac{2\sqrt{3}}{3}$cosA,解得:tanA=$\frac{\sqrt{3}}{3}$,
∴由A∈(0,π),可得:A=$\frac{π}{6}$.
(Ⅱ)∵cosA=$\frac{1}{3}$,b=3c,
∴a2=b2+c2-2bccosA=8c2,
∴a=$2\sqrt{2}$c,而sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{2\sqrt{2}}{3}$,
由正弦定理得:$\frac{2\sqrt{2}c}{sinA}=\frac{c}{sinC}$,
∴sinC=$\frac{1}{3}$.
点评 本题主要考查了两角和的正弦函数公式,特殊角的三角函数值,同角三角函数基本关系式,正弦定理,余弦定理的综合应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
相关题目
11.已知命题p:对任意x∈R,总有|x|≥0;命题q:x=2是方程x+2=0的根.则下列命题为真命题的是( )
| A. | p∧¬q | B. | ¬p∧q | C. | ¬p∧¬q | D. | p∧q |
12.一个几何体的三视图如图所示,则这个几何体外接球的体积为( )
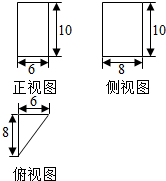

| A. | 1000$\sqrt{2}$π | B. | 200π | C. | $\frac{200}{3}$π | D. | $\frac{1000\sqrt{2}}{3}$π |
9.已知函数f(x)=sinx+cosx,则下列结论正确的是( )
| A. | 函数f(x)的图象关于直线$x=-\frac{π}{4}$对称 | B. | 函数f(x)的最大值为2 | ||
| C. | 函数f(x)在区间$(-\frac{π}{4},\frac{π}{4})$上是增函数 | D. | 函数f(x)的最小正周期为π |
16.cos40°sin20°+sin140°cos20°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
6.在数列{an}中,a3=1,an=an+1+1,n∈N*,则a10=( )
| A. | -6 | B. | -5 | C. | 5 | D. | 6 |
13.已知函数f(x)=2sinxcosx+1-2cos2(x-$\frac{π}{12}$),(x∈R),则下列结论正确的是( )
| A. | 周期T=2π | B. | f(x)向左平移$\frac{π}{6}$后是奇函数 | ||
| C. | 一个对称中心是($\frac{π}{3}$,0) | D. | 一条对称轴是x=$\frac{π}{6}$ |