题目内容
2.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的最小正周期为π,且图象过点($\frac{π}{6}$,$\frac{1}{2}$),函数g(x)=f(x)f(x-$\frac{π}{4}$)的单调递增区间[$\frac{kπ}{2}$-$\frac{π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$],k∈Z.分析 由条件利用正弦函数的周期性求得ω的值可得函数的解析式,再利用二倍角公式、诱导公式化简,利用正弦函数的单调性求得函数的增区间.
解答 解:函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的最小正周期为$\frac{2π}{ω}$=π,∴ω=2.
再根据图象过点($\frac{π}{6}$,$\frac{1}{2}$),可得sin(2•$\frac{π}{6}$+φ)=$\frac{1}{2}$,∴2•$\frac{π}{6}$+φ=$\frac{5π}{6}$,∴φ=$\frac{π}{2}$,f(x)=sin(2x+$\frac{π}{2}$)=cos2x.
函数g(x)=f(x)f(x-$\frac{π}{4}$)=cos2xcos2(x-$\frac{π}{4}$)=sin2xcos2x=$\frac{1}{2}$sin4x.
令2kπ-$\frac{π}{2}$≤4x≤2kπ+$\frac{π}{2}$,求得$\frac{kπ}{2}$-$\frac{π}{8}$≤x≤$\frac{kπ}{2}$+$\frac{π}{8}$,故函数的增区间为[$\frac{kπ}{2}$-$\frac{π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$],k∈Z.
故答案为:[$\frac{kπ}{2}$-$\frac{π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$],k∈Z.
点评 本题主要考查正弦函数的周期性、单调性,二倍角公式、诱导公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.一个几何体的三视图如图所示,则这个几何体外接球的体积为( )
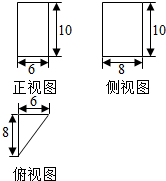

| A. | 1000$\sqrt{2}$π | B. | 200π | C. | $\frac{200}{3}$π | D. | $\frac{1000\sqrt{2}}{3}$π |
13.已知函数f(x)=2sinxcosx+1-2cos2(x-$\frac{π}{12}$),(x∈R),则下列结论正确的是( )
| A. | 周期T=2π | B. | f(x)向左平移$\frac{π}{6}$后是奇函数 | ||
| C. | 一个对称中心是($\frac{π}{3}$,0) | D. | 一条对称轴是x=$\frac{π}{6}$ |
12.下列关于不等式的结论中正确的是( )
| A. | 若a>b,则ac2>bc2 | B. | 若a>b,则a2>b2 | ||
| C. | 若a<b<0,则a2<ab<b2 | D. | 若a<b<0,则$\frac{a}{b}$>$\frac{b}{a}$ |