题目内容
 如图,半圆O是一个湖面的平面示意图,其直径AB=8百米,为了便与游
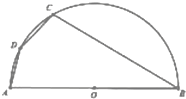
如图,半圆O是一个湖面的平面示意图,其直径AB=8百米,为了便与游客观光休闲,拟在观光区铺设一条从入口A到出口B的观光栈道,栈道由线段AD、线段DC及线段CB组成.其中点C为弧BD上一点,且线段AD=2百米.
(1)若线段CD=2百米,求线段BC的长;
(2)求整个观光栈道的最大值.
考点:余弦定理
专题:解三角形
分析:(1)连接BD,利用圆周角定理得到AD垂直于BD,在直角三角形ADB中,利用勾股定理求出BD的长,表示出sin∠ABD的值,利用等边对等角得到∠CBD=∠ABD,确定出cos∠CBD的值,利用余弦定理列出关系式,求出BC的长即可;
(2)由y=AD+DC+CB,利用正弦定理表示出DC与CB,利用两角和与差的正弦函数公式化为一个角的正弦函数,由正弦函数的值域确定出最大值即可.
(2)由y=AD+DC+CB,利用正弦定理表示出DC与CB,利用两角和与差的正弦函数公式化为一个角的正弦函数,由正弦函数的值域确定出最大值即可.
解答:
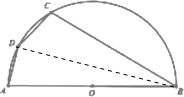 解:(1)连接BD,则AD⊥BD,
解:(1)连接BD,则AD⊥BD,
在Rt△ADB中,AD=2百米,AB=8百米,
根据勾股定理得:BD=
=2
(百米),sin∠ABD=
=
,
∵AD=CD=4百米,
∴∠CBD=∠ABD,
∴cos∠CBD=cos∠ABD=
=
,
在△BCD中,由余弦定理得:CD2=BD2+BC2-2BD•BC•cos∠CBD,即4=60+BC2-2×2
•BC•
,
解得:BC=7或8,
∵点C为弧BD上一点,
∴BC=7百米;
(2)令y=AD+DC+CB,sinC=sin(π-A)=sinA=
,cosC=cos(π-A)=-cosA=-
,
由正弦定理
=
=
=
=8,
DC=8sin∠CBD,CB=8sin∠CDB,
y=AD+DC+CB=2+8sin∠CBD+8sin∠CDB
=2+8sinα+8sin(π-α-C)
=2+8sinα+8sin(α+C)
=2+6sinα+2
cosα
=2+4
sin(α+θ)(其中cosθ=
,sinθ=
),
∴y=AD+DC+CB的最大值为2+4
,
则整个观光栈道的最大值为(2+4
)百米.
 解:(1)连接BD,则AD⊥BD,
解:(1)连接BD,则AD⊥BD,在Rt△ADB中,AD=2百米,AB=8百米,
根据勾股定理得:BD=
| 82-22 |
| 15 |
| AD |
| AB |
| 1 |
| 4 |
∵AD=CD=4百米,
∴∠CBD=∠ABD,
∴cos∠CBD=cos∠ABD=
| 1-sin2∠ABD |
| ||
| 4 |
在△BCD中,由余弦定理得:CD2=BD2+BC2-2BD•BC•cos∠CBD,即4=60+BC2-2×2
| 15 |
| ||
| 4 |
解得:BC=7或8,
∵点C为弧BD上一点,
∴BC=7百米;
(2)令y=AD+DC+CB,sinC=sin(π-A)=sinA=
| ||
| 4 |
| 1 |
| 4 |
由正弦定理
| BD |
| sinC |
| DC |
| sin∠CBD |
| CB |
| sin∠CDB |
2
| ||||
|
DC=8sin∠CBD,CB=8sin∠CDB,
y=AD+DC+CB=2+8sin∠CBD+8sin∠CDB
=2+8sinα+8sin(π-α-C)
=2+8sinα+8sin(α+C)
=2+6sinα+2
| 15 |
=2+4
| 6 |
| 6 | ||
4
|
2
| ||
4
|
∴y=AD+DC+CB的最大值为2+4
| 6 |
则整个观光栈道的最大值为(2+4
| 6 |
点评:此题考查了正弦、余弦定理,以及同角三角函数间的基本关系,熟练掌握定理是解本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
如果执行如图所示的框图,则输出n的值为( )


| A、9 | B、8 | C、7 | D、6 |
函数f(x)=cosx-
sinx的一条对称轴方程是( )
| 3 |
A、x=
| ||
B、x=
| ||
C、x=-
| ||
D、x=
|
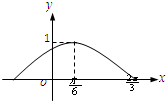
已知函数f(x)=sin(ωx+φ)(ω>0,-
<φ<
),其部分图象如图所示,则ω,φ的值分别为( )
| π |
| 2 |
| π |
| 2 |

A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=
| ||
D、ω=1,φ=
|
 如图所示,A,B是两圆的交点,AC是小圆的直径,D,E分别是CA,CB的延长线于大圆的交点,已知AC=4,BE=10,且BC=AD,则AB=
如图所示,A,B是两圆的交点,AC是小圆的直径,D,E分别是CA,CB的延长线于大圆的交点,已知AC=4,BE=10,且BC=AD,则AB=