题目内容

已知正项等差数列{an}的前n项和为Sn，S9=2，p，q∈N*，且p+q=18，则Sp•Sq的最大值为
 
．
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由等差数列的求和公式可得Sp•Sq=
pq
4
•(a1+ap)•(a1+aq)，由基本不等式可得．
解答： 解：Sp•Sq=
p(a1+ap)
2
•
q(a1+aq)
2

=
pq
4
•(a1+ap)•(a1+aq)
≤
1
4
(
p+q
2
)2•[a12+a1(ap+aq)+ap•aq]
≤
1
4
(
p+q
2
)2•[a12+a1(ap+aq)+(
ap+aq
2
)2]
=
1
4
(
p+q
2
)2•(a1+
ap+aq
2
)2=
1
4
(
18
2
)2•(a1+
2a9
2
)2

又∵S9=
9(a1+a9)
2
=2，∴a1+a9=
4
9
，
代入上式得：Sp•Sq≤4．
当且仅当p=q=9且ap=aq时取等号．
故答案为：4．
点评：本题考查等差数列的求和公式，涉及基本不等式求最值，属基础题．
练习册系列答案
相关题目
若正项数列{an}的前n项和Sn满足2an•Sn=an2+1（n∈N+），则通项an=
 
．
已知动圆过定点A（2，0），且在y轴上截得的弦长|MN|=4．
（Ⅰ）求动圆圆心C的轨迹方程；
（Ⅱ）若过点（1，0）的直线l交圆心C的轨迹于点A，B，且|AB|=5，求直线AB的方程．
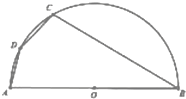如图，半圆O是一个湖面的平面示意图，其直径AB=8百米，为了便与游
客观光休闲，拟在观光区铺设一条从入口A到出口B的观光栈道，栈道由线段AD、线段DC及线段CB组成．其中点C为弧BD上一点，且线段AD=2百米．
（1）若线段CD=2百米，求线段BC的长；
（2）求整个观光栈道的最大值．
△ABC的三个内角A，B，C所对的边分别为a，b，c，若C=2A，cosA=
3
4
，
BA
•
BC
=
27
2
，
（1）求cosB；
（2）求边AC的长．
已知函数f（x）=
1
2
（ax-a-x），g（x）=
1
2
（ax+a-x），求证：[f（x）]2+[g（x）]2=g（2x）．
由集合A={0，1}所有真子集为元素构成的集合为M，则M=
 
．
已知一次函数y=kx-k+4的图象与y轴的交点坐标是（0，-2），那么这个一次函数的表达式是
 
．
计算：
（1）（
1
300
） -
1
2
+10（
3
25
） 
1
2
×（
27
16
） 
1
4
-
10
2-
3

（2）
1
2
lg
32
49
-
4
3
lg
8
+lg
245
+2 1+log23．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网