题目内容
设两个命题:p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立,q:函数f(x)=-(4-2a)x在(-∞,+∞)上是减函数,若命题p∨q为真,p∧q为假,则实数a的取值范围是多少?
考点:复合命题的真假
专题:简易逻辑
分析:根据一元二次不等式的解和判别式△的关系,及指数函数的单调性即可求出命题p,q下的a的取值范围,由p∨q为真,p∧q为假知p,q一真一假,所以分成p真q假,p假q真两种情况,分别求出a的取值范围再求并集即可.
解答:
解:p:△=4a2-16<0,解得-2<a<2;
q:首先4-2a>0,∴a<2;
函数f(x)=-(4-2a)x在(-∞,+∞)上是减函数,则4-2a>1,∴a<
;
若命题p∨q为真,p∧q为假,则p,q一真一假;
若p真q假,则:
,∴
≤a<2;
若p假q真,则:
,∴a≤-2;
综上得a的取值范围是[
,2)∪(-∞,-2].
q:首先4-2a>0,∴a<2;
函数f(x)=-(4-2a)x在(-∞,+∞)上是减函数,则4-2a>1,∴a<
| 3 |
| 2 |
若命题p∨q为真,p∧q为假,则p,q一真一假;
若p真q假,则:
|
| 3 |
| 2 |
若p假q真,则:
|
综上得a的取值范围是[
| 3 |
| 2 |
点评:考查一元二次不等式的解和判别式△的关系,指数函数的单调性,p∨q,p∧q的真假和p,q真假的关系.

练习册系列答案
相关题目
已知集合M={a2,a}.P={-a,2a-1};若card(M∪P)=3,则M∩P=( )
| A、{-1} | B、{1} |
| C、{0} | D、{3} |
已知等比数列{an}满足a3a5=2,则a1a42a7的值是( )
| A、2 | B、4 | C、8 | D、16 |
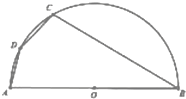 如图,半圆O是一个湖面的平面示意图,其直径AB=8百米,为了便与游
如图,半圆O是一个湖面的平面示意图,其直径AB=8百米,为了便与游