题目内容
函数f(x)=1-
(x≠0,x≠1),非空集合A满足x∈A则f(x)∈A.
(1)当2∈A求集合A;
(2)求出非空集合A中的元素;
(3)证明非空集合A中必含有负数元素.
| 1 |
| x |
(1)当2∈A求集合A;
(2)求出非空集合A中的元素;
(3)证明非空集合A中必含有负数元素.
考点:元素与集合关系的判断
专题:集合
分析:(1)把x=2代入,求出f(2)=
,把x=
代入,求出f(
)=-1,把x=-1代入,求出f(-1)=2,出现循环,从而求出A中的元素;
(2)设a∈A,得出f(a)=
∈A,把x=
代入,求出f(
)=-
∈A,把x=-
代入,求出f(-
)=a,出现循环,从而求出A中的元素;
(3)将A中的所有元素相乘得出-1<0,从而得出非空集合A中必含有负数元素.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)设a∈A,得出f(a)=
| a-1 |
| a |
| a-1 |
| a |
| a-1 |
| a |
| 1 |
| a-1 |
| 1 |
| a-1 |
| 1 |
| a-1 |
(3)将A中的所有元素相乘得出-1<0,从而得出非空集合A中必含有负数元素.
解答:
解:(1)x=2时,f(2)=1-
=
,
f(
)=1-2=-1,f(-1)=1-(-1)=2,
∴A={2,
,-1};
(2)设a∈A,∴f(a)=1-
=
∈A,
∴f(
)=1-
=-
∈A,
∴f(-
)=a,
∴A={a,
,-
};
(3)由(2)得:a•
•(-
)=-1,
∴非空集合A中必含有负数元素.
| 1 |
| 2 |
| 1 |
| 2 |
f(
| 1 |
| 2 |
∴A={2,
| 1 |
| 2 |
(2)设a∈A,∴f(a)=1-
| 1 |
| a |
| a-1 |
| a |
∴f(
| a-1 |
| a |
| a |
| a-1 |
| 1 |
| a-1 |
∴f(-
| 1 |
| a-1 |
∴A={a,
| a-1 |
| a |
| 1 |
| a-1 |
(3)由(2)得:a•
| a-1 |
| a |
| 1 |
| a-1 |
∴非空集合A中必含有负数元素.
点评:本题考查了元素和集合的关系,可采用迭代法求出集合中的元素,是一道中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
直线平分圆x2+y2-2x-4y+1=0的周长,则此直线的方程可能是( )
| A、x-y+1=0 |
| B、x+y+3=0 |
| C、x+y-1=0 |
| D、x-y+3=0 |
已知集合M={a2,a}.P={-a,2a-1};若card(M∪P)=3,则M∩P=( )
| A、{-1} | B、{1} |
| C、{0} | D、{3} |
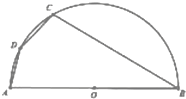 如图,半圆O是一个湖面的平面示意图,其直径AB=8百米,为了便与游
如图,半圆O是一个湖面的平面示意图,其直径AB=8百米,为了便与游