题目内容
设点P是函数y=-
图象上的任意一点，点Q（2a，a-3）（a∈R），则|PQ|的最小值为（ ）
| 4-(x-1)2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：函数的最值及其几何意义
专题：综合题,直线与圆
分析：将函数进行化简，得到函数对应曲线的特点，利用直线和圆的性质，即可得到结论．
解答：
解：由函数y=-
得（x-1）2+y2=4，（y≤0），对应的曲线为圆心在C（1，0），半径为2的圆的下部分，
∵点Q（2a，a-3），
∴x=2a，y=a-3，消去a得x-2y-6=0，
即Q（2a，a-3）在直线x-2y-6=0上，
过圆心C作直线的垂线，垂足为A，
则|PQ|min=|CA|-2=
-2=
-2，
故选：C．
| 4-(x-1)2 |
∵点Q（2a，a-3），
∴x=2a，y=a-3，消去a得x-2y-6=0，
即Q（2a，a-3）在直线x-2y-6=0上，
过圆心C作直线的垂线，垂足为A，
则|PQ|min=|CA|-2=
| |1-0-6| | ||
|
| 5 |
故选：C．
点评：本题主要考查直线和圆的位置关系的应用，根据函数的表达式确定对应曲线是解决本题的关键．
练习册系列答案
相关题目
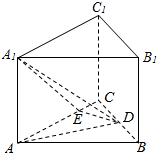如图，在正三棱柱ABC-A1B1C1中，AB=4，AA1=| 7 |
（1）证明：平面A1DE⊥平面ACC1A1；
（2）求直线AD和平面A1DE所成角的正弦值．
设A、B、C、D是球面上的四点，AB、AC、AD两两互相垂直，且AB=5，AC=4，AD=
，则球的表面积为（ ）
| 23 |
| A、36π | B、64π |
| C、100π | D、144π |
若圆C的半径为1，点C与点（2，0）关于点（1，0）对称，则圆C的标准方程为（ ）
| A、x2+y2=1 |
| B、（x-3）2+y2=1 |
| C、（x-1）2+y2=1 |
| D、x2+（y-3）2=1 |
f（x）=
+log4（x+1）的定义域是（ ）
| ||
| x-1 |
| A、（0，1）∪（1，4] |
| B、[-1，1）∪（1，4] |
| C、（-1，4） |
| D、（-1，1）∪（1，4] |