题目内容
对于任意实数a(a≠0)和b,不等式|a+b|+|2a-b|≥|b|(|x-1|+|x-2|)恒成立,试求实数x的取值范围.
考点:绝对值三角不等式
专题:计算题,不等式的解法及应用
分析:分类讨论,当b≠0时,|x-1|+|x-2|≤
恒成立,故|x-1|+|x-2|小于或等于
的最小值,即可得出结论.
| |a+b|+|2a-b| |
| |b| |
| |a+b|+|2a-b| |
| |b| |
解答:
解:(1)当b=0时,原不等式恒成立,则x∈R.
(2)当b≠0时,|x-1|+|x-2|≤
恒成立,故|x-1|+|x-2|小于或等于
的最小值.
设t=
,则
=|t+1|+|2t-1|=
,
∴t=
时,取到最小值
,
∴|x-1|+|x-2|≤
,|x-1|+|x-2|表示数轴上的x对应点到1和2对应点的距离之和,
故不等式的解集为[
,
].
(2)当b≠0时,|x-1|+|x-2|≤
| |a+b|+|2a-b| |
| |b| |
| |a+b|+|2a-b| |
| |b| |
设t=
| a |
| b |
| |a+b|+|2a-b| |
| |b| |
|
∴t=
| 1 |
| 2 |
| 3 |
| 2 |
∴|x-1|+|x-2|≤
| 3 |
| 2 |
故不等式的解集为[
| 3 |
| 4 |
| 9 |
| 4 |
点评:本题考查绝对值的意义,绝对值不等式的解法,判断|x-1|+|x-2|表示数轴上的x对应点到1和2对应点的距离之和,是解题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
已知集合P={x|-1≤x≤1},M={a},若P∪M=P,则a的取值范围是( )
| A、(-∞,-1] |
| B、[1,+∞) |
| C、[-1,1] |
| D、(-∞,-1]∪[1,+∞) |
已知数列{an}中,a1=1,以后各项由公式a1•a2•a3…an=n2,则a3+a5=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知四个函数:①y=f1(x)②y=f2(x)③y=f3(x)④y=f4(x)的图象分别如图所示,则下列等式成立的是( )
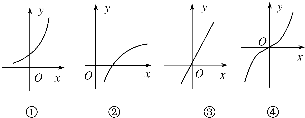

| A、f1(x1+x2)=f1(x1)+f1(x2) |
| B、f2(x1+x2)=f2(x1)+f2(x2) |
| C、f3(x1+x2)=f3(x1)+f3(x2) |
| D、f4(x1+x2)=f4(x1)+f4(x2) |
下列说法正确的个数是( )
①平行于同一直线的两条直线平行
②平行于同一平面的两个平面平行
③两条平行线中的一条和一个平面平行,则另一条也与这个平面平行
④一条直线与两个平行平面中的一个平面平行,则这条直线与另一平面也平行.
①平行于同一直线的两条直线平行
②平行于同一平面的两个平面平行
③两条平行线中的一条和一个平面平行,则另一条也与这个平面平行
④一条直线与两个平行平面中的一个平面平行,则这条直线与另一平面也平行.
| A、1 | B、2 | C、3 | D、4 |
已知{an}是公差不为0的等差数列,a1=2且a2,a4,a8成等比数列,若bn=
,则数列{bn}的前n项和的取值范围是( )
| 2 |
| n(an+2) |
A、[
| ||
| B、(0,1) | ||
C、(0,
| ||
| D、(1,+∞) |
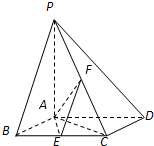 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.