题目内容
7.△ABC的内角A,B,C的对边分别为a,b,c,已知a=bcosC+csinB(1)求角B的大小;
(2)若$b=4,C=\frac{π}{3}$,求△ABC的面积.
分析 (1)由正弦定理,两角和的正弦函数公式可求cosBsinC=sinCsinB,结合sinC≠0,利用同角三角函数基本关系式可求tanB=1,结合范围B∈(0,π),可求B的值.
(2)由(1)及三角形内角和定理可求A,利用正弦定理可求c的值,根据三角形面积公式即可计算得解.
解答 (本题满分为12分)
解:(1)∵a=bcosC+csinB,
∴由正弦定理可得:sinA=sinBcosC+sinCsinB,
∴sin(B+C)=sinBcosC+sinCcosB,即cosBsinC=sinCsinB,
∵sinC≠0,
∴cosB=sinB,
∴$tanB=\frac{sinB}{cosB}=1$,B∈(0,π),
∴B=$\frac{π}{4}$.…(6分)
(2)由(1)可得$A=π-B-C=\frac{5π}{12}$,
由正弦定理可得:$\frac{a}{sinA}=\frac{c}{sinC}=\frac{b}{sinB}=\frac{2}{{sin\frac{π}{4}}}=2\sqrt{2}$,
∴$c=2\sqrt{6}$,
∴${S_{△ABC}}=\frac{1}{2}bcsinA=6+2\sqrt{3}$.…(12分)
点评 本题主要考查了正弦定理,两角和的正弦函数公式,同角三角函数基本关系式,三角形内角和定理,三角形面积公式在解三角形中的综合应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
15. “牟合方盖”是我国古代数学家刘微在研究球的体积的过程中构造的一个和谐优美的几何体,它由完全相同的四个曲面构成,相对的两个曲面在同一圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).如图,正边形ABCD是为体现其直观性所作的辅助线,若该几何体的正视图与侧视图都是半径为r的圆,根据祖暅原理,可求得该几何体的体积为( )
“牟合方盖”是我国古代数学家刘微在研究球的体积的过程中构造的一个和谐优美的几何体,它由完全相同的四个曲面构成,相对的两个曲面在同一圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).如图,正边形ABCD是为体现其直观性所作的辅助线,若该几何体的正视图与侧视图都是半径为r的圆,根据祖暅原理,可求得该几何体的体积为( )
 “牟合方盖”是我国古代数学家刘微在研究球的体积的过程中构造的一个和谐优美的几何体,它由完全相同的四个曲面构成,相对的两个曲面在同一圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).如图,正边形ABCD是为体现其直观性所作的辅助线,若该几何体的正视图与侧视图都是半径为r的圆,根据祖暅原理,可求得该几何体的体积为( )
“牟合方盖”是我国古代数学家刘微在研究球的体积的过程中构造的一个和谐优美的几何体,它由完全相同的四个曲面构成,相对的两个曲面在同一圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).如图,正边形ABCD是为体现其直观性所作的辅助线,若该几何体的正视图与侧视图都是半径为r的圆,根据祖暅原理,可求得该几何体的体积为( )| A. | $\frac{8}{3}{r^3}$ | B. | $\frac{8}{3}π{r^3}$ | C. | $\frac{16}{3}{r^3}$ | D. | $\frac{16}{3}π{r^3}$ |
2.设向量$\overrightarrow a$,$\overrightarrow b$不平行,向量$λ\overrightarrow a+\overrightarrow b$与$\overrightarrow a+2\overrightarrow b$平行,则实数λ等于( )
| A. | 2 | B. | 4 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
12.观察下列各式:1=12,2+3+4=32,3+4+5+6=52,4+5+6+7+8+9+10=72,…,可以得出的一般结论是( )
| A. | n+(n+1)+(n+2)+…+(3n-2)=n2 | B. | n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2 | ||
| C. | n+(n+1)+(n+2)+…+(3n-1)=n2 | D. | n+(n+1)+(n+2)+…+(3n-1)=(2n-1)2 |
19.在等差数列{an}中,已知a2+a5=4,an=33,a1=$\frac{1}{3}$,则n是( )
| A. | 48 | B. | 49 | C. | 50 | D. | 51 |
16.某几何体的三视图如图所示,则该几何体的体积为( )
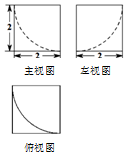

| A. | $8-\frac{4}{3}π$ | B. | $8-\frac{8}{3}π$ | C. | 24-π | D. | 24+π |
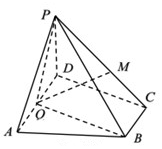 如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.