题目内容
7.函数f(x)的部分图象如图所示,则f(x)的解析式可以是( )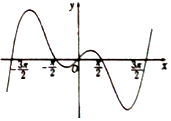
| A. | f(x)=x+sinx | B. | f(x)=$\frac{cosx}{x}$ | C. | f(x)=x(x-$\frac{π}{2}$)(x-$\frac{3π}{2}$) | D. | f(x)=xcosx |
分析 判断函数的奇偶性排除选项,然后利用函数的零点与函数的定义域,推出结果即可.
解答 解:由函数的图形可知函数是奇函数,排除C,
又f(x)=x+sinx=0,函数只有一个零点,所以A不正确;
函数的图象可知,x=0是函数的零点,而f(x)=$\frac{cosx}{x}$,x≠0,所以B不正确;
故选:D.
点评 本题考查函数的图象的判断与应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.有5名高中优秀毕业生回母校成都7中参加高2015级励志成才活动,到3个班去做学习经验交流,则每个班至少去一名的不同分派方法种数为( )
| A. | 200 | B. | 180 | C. | 150 | D. | 280 |
19.《张丘建算经》是我国古代数学名著,书中有如下问题:“今有女不善织布,每天所织的布以同数递减,初日织五尺,末日织一尺,共织三十日,问共织几何?”其意思是:“一女子织布30天,每天所织布的数以相同的数递减,第一天织布5尺,最后一天织布1尺,则30天共织布多少尺?”那么该女子30天共织布( )
| A. | 70尺 | B. | 80尺 | C. | 90尺 | D. | 100尺 |
16.若变量x,y满足不等式组$\left\{\begin{array}{l}y≤2\\ x+y≥1\\ x-y≤a\end{array}\right.$,且z=3x-y的最大值为7,则实数a的值为( )
| A. | 1 | B. | 7 | C. | -1 | D. | -7 |
17.已知f(x)=2sin2x+2sinxcosx,则f(x)的最小正周期和一个单调减区间分别为( )
| A. | 2π,[$\frac{3π}{8}$,$\frac{7π}{8}$] | B. | π,[$\frac{3π}{8}$,$\frac{7π}{8}$] | C. | 2π,[-$\frac{π}{8}$,$\frac{3π}{8}$] | D. | π,[-$\frac{π}{8}$,$\frac{3π}{8}$] |
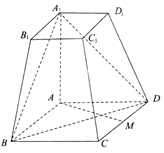 如图所示,在四棱台ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2.
如图所示,在四棱台ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2. 一个几何体的三视图如图所示,图中矩形均为边长是1的正方形弧线为四分之一圆,则该几何体的体积是$1-\frac{π}{6}$.
一个几何体的三视图如图所示,图中矩形均为边长是1的正方形弧线为四分之一圆,则该几何体的体积是$1-\frac{π}{6}$.