题目内容
19．《张丘建算经》是我国古代数学名著，书中有如下问题：“今有女不善织布，每天所织的布以同数递减，初日织五尺，末日织一尺，共织三十日，问共织几何？”其意思是：“一女子织布30天，每天所织布的数以相同的数递减，第一天织布5尺，最后一天织布1尺，则30天共织布多少尺？”那么该女子30天共织布（ ）| A． | 70尺 | B． | 80尺 | C． | 90尺 | D． | 100尺 |
分析 设该女子每天所织布的数以d尺的数递减，由第一天织布5尺，最后一天织布1尺，利用等差数列通项公式求出d=-$\frac{4}{29}$，由此利用等差数列求和公式能求出30天共织布多少尺．
解答 解：设该女子每天所织布的数以d尺的数递减，
∵一女子织布30天，每天所织布的数以相同的数d递减，
第一天织布5尺，最后一天织布1尺，
∴a30=5+29d=1，解得d=-$\frac{4}{29}$，
∴30天共织布：S30=30×5+$\frac{30×29}{2}×（-\frac{4}{29}）$=90（尺）．
故选：C．
点评 本题考查等差数列的前30项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
9．在长方体ABCD-A1B1C1D1中，AB=BC=4，AA1=2，则直线BC1与平面BB1D1D所成角的正弦值为（ ）
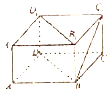
| A． | $\frac{{\sqrt{6}}}{3}$ | B． | $\frac{{2\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{15}}}{5}$ | D． | $\frac{{\sqrt{10}}}{5}$ |
10．已知函数f（x）是定义在实数集R上的奇函数，若x＞0时，f（x）=x•ex，则不等式f（x）＞3x的解集为（ ）
| A． | {x|-ln3＜x＜ln3} | B． | {x|x＜-ln3，或x＞ln3} | ||
| C． | {x|-ln3＜x＜0，或x＞ln3} | D． | {x|x＜-ln3，或0＜x＜ln3} |
7．函数f（x）的部分图象如图所示，则f（x）的解析式可以是（ ）
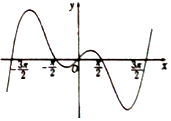
| A． | f（x）=x+sinx | B． | f（x）=$\frac{cosx}{x}$ | C． | f（x）=x（x-$\frac{π}{2}$）（x-$\frac{3π}{2}$） | D． | f（x）=xcosx |
14．设i是虚数单位，复数i（1+ai）为纯虚数，则实数a为（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
8．
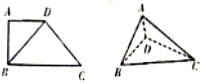如图所示，在四边形ABCD中，AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°，将△ABD沿BD折起，使得平面ABD⊥平面BCD，构成四面体A-BCD，则在四面体中，下列说法正确的是（ ）
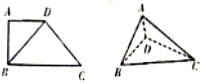如图所示，在四边形ABCD中，AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°，将△ABD沿BD折起，使得平面ABD⊥平面BCD，构成四面体A-BCD，则在四面体中，下列说法正确的是（ ）| A． | 平面ABD⊥平面ABC | B． | 平面ACD⊥平面BCD | C． | 平面ABC⊥平面BCD | D． | 平面ACD⊥平面ABC |