题目内容
8．若曲线f（x）=x3+x-2在点P0处的切线垂直于直线x+4y+3=0，则点P0的坐标为（ ）| A． | （1，0） | B． | （2，8） | C． | （2，8）或（-1，-4） | D． | （1，0）或（-1，-4） |
分析 设P0（m，n），求出f（x）的导数，求得切线的斜率，由两直线垂直的条件，解方程可得m，进而得到n，可得切点的坐标．
解答 解：设P0（m，n），f（x）的导数为f′（x）=3x2+1，
即有在点P0处的切线的斜率为k=3m2+1，
由切线垂直于直线x+4y+3=0，可得3m2+1=4，
解得m=±1，
可得m=1，n=0或m=-1，n=-4．
即P0（1，0），或（-1，-4）．
故选：D．
点评 本题考查导数的运用：求切线的斜率，考查导数的几何意义，同时考查两直线垂直的条件：斜率之积为-1，属于基础题．
练习册系列答案
考前必练系列答案
相关题目
16．给出下面四个命题（其中m，n，l为空间中不同的三条直线，α，β为空间中不同的两个平面）：
①m∥n，n∥α⇒m∥α
②α⊥β，α∩β=m，l⊥m⇒l⊥β；
③l⊥m，l⊥n，m?α，n?α⇒l⊥α
④m∩n=A，m∥α，m∥β，n∥α，n∥β⇒α∥β．
其中错误的命题个数为（ ）
①m∥n，n∥α⇒m∥α
②α⊥β，α∩β=m，l⊥m⇒l⊥β；
③l⊥m，l⊥n，m?α，n?α⇒l⊥α
④m∩n=A，m∥α，m∥β，n∥α，n∥β⇒α∥β．
其中错误的命题个数为（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
13．不等式组$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-y+1≥0}\\{2x+3y-4≤0}\end{array}\right.$，表示的平面区域绕着原点旋转一周所得到的平面图形的面积为（ ）
| A． | $\frac{12π}{25}$ | B． | $\frac{17π}{25}$ | C． | 3π | D． | $\frac{16π}{5}$ |
20．下列说法中，正确的是（ ）
| A． | 命题“若x≠2或y≠7，则x+y≠9”的逆命题为真命题 | |
| B． | 命题“若x2=4，则x=2”的否命题是“若x2=4，则x≠2” | |
| C． | 命题“若x2＜1，则-1＜x＜1”的逆否命题是“若x＜-1或x＞1，则x2＞1” | |
| D． | 若命题p：?x∈R，x2-x+1＞0，q：?x0∈（0，+∞），sinx0＞1，则（￢p）∨q为真命题 |
18．
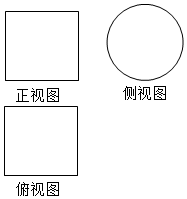如图所示，一个空间几何体的正视图和俯视图都是边长为2的正方形，侧视图是一个直径为2的圆，则该几何体的表面积是（ ）
如图所示，一个空间几何体的正视图和俯视图都是边长为2的正方形，侧视图是一个直径为2的圆，则该几何体的表面积是（ ）| A． | 4π | B． | 6π | C． | 8π | D． | 16π |