题目内容
9.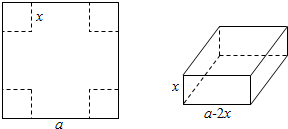 有一块边长为a的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方体形的无盖容器,为使其容积最大,截下的小正方形边长应为多少?
有一块边长为a的正方形铁板,现从铁板的四个角各截去一个相同的小正方形,做成一个长方体形的无盖容器,为使其容积最大,截下的小正方形边长应为多少?
分析 无盖容器的底边长为a-2x,无盖容器的高为x,可得出容积V(x)与自变量x之间的关系式,由a-2x>0,可求出V(x)的定义域;利用导数法,求出其函数值取最大值时,自变量x的值,即可得到要使无盖容器的容积最大.
解答 解:设小正方形的边长为x,由题意,无盖容器的底边长为a-2x,无盖容器的高为x,
可得无盖容器的容积是V(x)与x的函数关系式是:
V(x)=(a-2x)2•x,且V(x)的定义域为(0,$\frac{a}{2}$),
导数V′(x)=(a-2x)2-4x(a-2x)=(a-2x)(a-6x),
令V′(x)=0,则x=$\frac{a}{6}$,或x=$\frac{a}{2}$(舍),
由函数在(0,$\frac{a}{6}$)上单调递增,在($\frac{a}{6}$,$\frac{a}{2}$)上单调递减,
可得截下的小正方形边长为$\frac{a}{6}$时,无盖容器的容积取得最大为$\frac{2{a}^{3}}{27}$.
点评 本题考查函数模型的选择与应用,解题的关键是设出自变量并根据已知条件确定出函数的解析式和定义域,将一个实际问题转化为函数问题,运用导数解决,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
20.下列说法中,正确的是( )
| A. | 命题“若x≠2或y≠7,则x+y≠9”的逆命题为真命题 | |
| B. | 命题“若x2=4,则x=2”的否命题是“若x2=4,则x≠2” | |
| C. | 命题“若x2<1,则-1<x<1”的逆否命题是“若x<-1或x>1,则x2>1” | |
| D. | 若命题p:?x∈R,x2-x+1>0,q:?x0∈(0,+∞),sinx0>1,则(¬p)∨q为真命题 |
1.已知二次函数y=f(x),当x=2时,函数f(x)取最小值-1,且f(1)+f(4)=3.
(1)求f(x)的解析式;
(2)若g(x)=f(x)-kx在区间(1,4)上无最小值,求实数k的取值范围.
(1)求f(x)的解析式;
(2)若g(x)=f(x)-kx在区间(1,4)上无最小值,求实数k的取值范围.
18.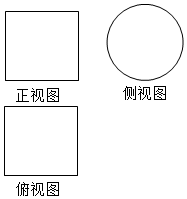 如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
 如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )
如图所示,一个空间几何体的正视图和俯视图都是边长为2的正方形,侧视图是一个直径为2的圆,则该几何体的表面积是( )| A. | 4π | B. | 6π | C. | 8π | D. | 16π |