题目内容
2.设f(x)是定义域为R且最小正周期为2π的函数,且有f(x)=$\left\{\begin{array}{l}{sinx,0≤x≤π}\\{cosx,-π<x<0}\end{array}\right.$,则f(-$\frac{13π}{4}$)=( )| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | 0 | D. | 1 |
分析 根据函数的周期性进行转化求解即可.
解答 解:∵f(x)是定义域为R且最小正周期为2π的函数,
∴f(-$\frac{13π}{4}$)=f(-$\frac{13π}{4}$+4π)=f($\frac{3π}{4}$),
∵f(x)=$\left\{\begin{array}{l}{sinx,0≤x≤π}\\{cosx,-π<x<0}\end{array}\right.$,
∴f($\frac{3π}{4}$)=sin$\frac{3π}{4}$=$\frac{\sqrt{2}}{2}$,
故选:A
点评 本题主要考查函数值的计算,根据函数的周期性进行转换求解是解决本题的关键.比较基础.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
12.向顶角为120°的等腰三角形ABC(其中AC=BC)内任意投一点M,则AM小于AC的概率为( )
| A. | $\frac{{\sqrt{3}π}}{3}$ | B. | $\frac{{\sqrt{3}π}}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{3}$ |
13.不等式组$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-y+1≥0}\\{2x+3y-4≤0}\end{array}\right.$,表示的平面区域绕着原点旋转一周所得到的平面图形的面积为( )
| A. | $\frac{12π}{25}$ | B. | $\frac{17π}{25}$ | C. | 3π | D. | $\frac{16π}{5}$ |
 如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=4,BC=$\frac{3}{2}$,CD=$\frac{5}{2}$,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.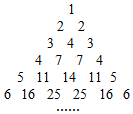 如图三角形数阵满足:
如图三角形数阵满足: