题目内容
17．
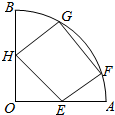如图，四边形EFGH是圆心角为60°，半径为R的扇形的内接矩形，点F，G在$\widehat{AB}$上，求四边形EFGH的最大面积．
分析 求最大值问题这里应构造函数，怎么选择便于以此表达矩形面积的自变量
解答 解：设∠FOA=θ，则GF=2Rsin（30°-θ），
在△OFE中，∠OEF=150°，故FE=2Rsinθ
设矩形的面积为S．
那么S=EF•FG=4R2sinθsin（30°-θ）
=2R2[cos（2θ-30°）-cos30°]=2R2[cos（2θ-30°）-$\frac{\sqrt{3}}{2}$]
又∵0＜θ＜30°，故当cos（2θ-30°）=1即θ=15°时，S取最大值R2（2-$\sqrt{3}$）．
点评 本题关键是如何利用角θ表示矩形的长与宽，合理地把长与宽放在三角形中，利用正弦定理或三角定义来表示．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
8．1.5 1.5 1.6 1.6 1.7的中位数和平均数是（ ）
| A． | 1.5 1.65 | B． | 1.6 1.58 | C． | 1.65 1.7 | D． | 1.7 1.7 |
5．当0＜x＜1时，幂函数y=xa的图象都在直线y=x的上方，则a的取值范围为（ ）
| A． | （-∞，0） | B． | （0，1） | C． | （-∞，1） | D． | （1，+∞） |
2．已知三棱锥P-ABC的四个顶点都在半径为2的球面上，且PA⊥平面ABC，若AB=2．AC=$\sqrt{3}$，∠BAC=$\frac{π}{2}$，则棱PA的长为（ ）
| A． | $\frac{3}{2}$ | B． | $\sqrt{3}$ | C． | 3 | D． | 9 |
6．一台机器按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，具有线性相关关系，下表为抽样试验的结果：
（1）如果y对x有线性相关关系，求回归方程；
（2）若实际生产中，允许每小时生产的产品中有缺点的零件最多有10个，那么机器的运转速度应控制在设么范围内？参考公式：$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．
| 转速x（转/秒） | 8 | 10 | 12 | 14 | 16 |
| 每小时生产有缺点的零件数y（件） | 5 | 7 | 8 | 9 | 11 |
（2）若实际生产中，允许每小时生产的产品中有缺点的零件最多有10个，那么机器的运转速度应控制在设么范围内？参考公式：$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．
8．设z=1+i（i是虚数单位），则$\frac{2}{z}$-$\overline{z}$=（ ）
| A． | i | B． | 2-i | C． | 1-i | D． | 0 |