题目内容
2.已知三棱锥P-ABC的四个顶点都在半径为2的球面上,且PA⊥平面ABC,若AB=2.AC=$\sqrt{3}$,∠BAC=$\frac{π}{2}$,则棱PA的长为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 9 |
分析 把三棱锥扩展为长方体,三棱锥的外接球就是长方体的外接球,长方体的体对角线就是球的直径.
解答 解:由三棱锥扩展为长方体,长方体的对角线的长为直径4,
因为AB=2.AC=$\sqrt{3}$,∠BAC=$\frac{π}{2}$,
所以4+3+PA2=16,
所以PA=3.
故选:C.
点评 本题考查直线与平面垂直的性质,球的内接几何体与球的关系,考查空间想象能力,计算能力.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
12.甲、乙、丙三人独立参加体育达标测试,已知甲、乙、丙各自通过测试的概率分别为$\frac{2}{3}$,$\frac{3}{4}$,p,且他们是否通过测试互不影响.若三人中只有甲通过的概率为$\frac{1}{16}$,则甲、丙二人中至少有一人通过测试的概率为( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{8}$ | D. | $\frac{6}{7}$ |
10.下列物理量:①质量;②速度;③位移;④力;⑤加速度;⑥路程;⑦功.其中不是向量的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.$\frac{(1+i)^{3}}{(1+i)^{2}}$等于( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
13.设z=1+i(i是虚数单位),则$\frac{2}{z}$=( )
| A. | i | B. | 2-i | C. | 1-i | D. | 0 |
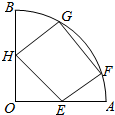 如图,四边形EFGH是圆心角为60°,半径为R的扇形的内接矩形,点F,G在$\widehat{AB}$上,求四边形EFGH的最大面积.
如图,四边形EFGH是圆心角为60°,半径为R的扇形的内接矩形,点F,G在$\widehat{AB}$上,求四边形EFGH的最大面积.