题目内容
12.设P是函数y=elnx上一点,Q是直线y=x+3上一点,则PQ的最小值为$\frac{3\sqrt{2}}{2}$.分析 由导数可得曲线的切线y=x+t的t值,由平行线间的距离公式可得所求.
解答 解:∵y=elnx,∴y′=$\frac{e}{x}$
设与直线y=x+3平行的直线与曲线y=elnx相切,
则可得直线的斜率1等于该点处的导数值$\frac{e}{{x}_{0}}$,
解得x0=e,∴y0=e,
把点(e,e)代入y=x+t可解得t=0,
∴两平行线y=x与y=x+3的距离d=$\frac{3}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$,
∴|PQ|的最小值为:$\frac{3\sqrt{2}}{2}$.
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查平行线间的距离公式,涉及曲线的切线的求解,属中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
3. 现有一矩形空地,准备将其划分成六个区域栽种四种不同颜色的花卉进行绿化,要求4、5、6三个区域中的任意两个都不能栽种相同颜色的花卉,而且相邻的两个区域也不能栽种相同的颜色的花卉,则不同的花卉栽种方式有( )
现有一矩形空地,准备将其划分成六个区域栽种四种不同颜色的花卉进行绿化,要求4、5、6三个区域中的任意两个都不能栽种相同颜色的花卉,而且相邻的两个区域也不能栽种相同的颜色的花卉,则不同的花卉栽种方式有( )
 现有一矩形空地,准备将其划分成六个区域栽种四种不同颜色的花卉进行绿化,要求4、5、6三个区域中的任意两个都不能栽种相同颜色的花卉,而且相邻的两个区域也不能栽种相同的颜色的花卉,则不同的花卉栽种方式有( )
现有一矩形空地,准备将其划分成六个区域栽种四种不同颜色的花卉进行绿化,要求4、5、6三个区域中的任意两个都不能栽种相同颜色的花卉,而且相邻的两个区域也不能栽种相同的颜色的花卉,则不同的花卉栽种方式有( )| A. | 288 | B. | 144 | C. | 216 | D. | 72 |
3.若$\frac{i}{1-i}$=a+bi(a,b∈R,i为虚数单位),则a-b等于( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | 0 | D. | -1 |
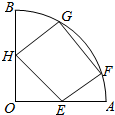 如图,四边形EFGH是圆心角为60°,半径为R的扇形的内接矩形,点F,G在$\widehat{AB}$上,求四边形EFGH的最大面积.
如图,四边形EFGH是圆心角为60°,半径为R的扇形的内接矩形,点F,G在$\widehat{AB}$上,求四边形EFGH的最大面积. 如图,在正四棱锥S-ABCD中,SA=2AB=2,M,N分别是棱SA,SC的中点,平面SBC∩平面SAD=l.
如图,在正四棱锥S-ABCD中,SA=2AB=2,M,N分别是棱SA,SC的中点,平面SBC∩平面SAD=l.