题目内容
7.已知函数f(x)=b+logax(a>0且a≠1)的图象过点(27,-1),其反函数的图象过点(1,3),则f(x)在[9,81]上的最大值为( )| A. | -1 | B. | 0 | C. | 1 | D. | 3 |
分析 根据反函数的性质可知f(x)过(3,1),把(27,-1)和(3,1)代入f(x)求出a,b,得到f(x)的解析式,判断f(x)在[9,81]上的单调性得出最大值.
解答 解:∵f(x)的反函数的图象过点(1,3),∴f(x)的图象过点(3,1),又∵f(x)的图象过点(27,-1),
∴$\left\{\begin{array}{l}{b+lo{g}_{a}3=1}\\{b+lo{g}_{a}27=-1}\end{array}\right.$,解得a=$\frac{1}{3}$,b=2.∴f(x)=2+log${\;}_{\frac{1}{3}}$x,∴f(x)在[9,81]上是减函数,∴fmax(x)=f(9)=0.
故选:B.
点评 本题考查了反函数的性质,对数函数的单调性,是中档题.

练习册系列答案
相关题目
17.已知抛物线x2=8y的焦点为F,在抛物线内有一点A(4,4),若该抛物线上存在一动点P,则|PA|+|PF|的最小值为( )
| A. | $4\sqrt{2}+2$ | B. | 4 | C. | $2\sqrt{5}$ | D. | 6 |
12.甲、乙、丙三人独立参加体育达标测试,已知甲、乙、丙各自通过测试的概率分别为$\frac{2}{3}$,$\frac{3}{4}$,p,且他们是否通过测试互不影响.若三人中只有甲通过的概率为$\frac{1}{16}$,则甲、丙二人中至少有一人通过测试的概率为( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{8}$ | D. | $\frac{6}{7}$ |
16.已知函数f(x)的定义域为[-2,2],对任意的x,y∈[-2,2],都有f(x+y)=f(x)+f(y),且当x>0时,有f(x)>0,f(1)=1,若不等式f(x)<logam(a>1)对任意的实数x∈[-2,2]恒成立,则实数m的取值范围是( )
| A. | [a2,+∞) | B. | (0,a2] | C. | (a2,+∞) | D. | (0,a2) |
 如图,△ABC的内切圆I切AB、BC、AC于点D、E、F.直线EF与AI、BI、DI交于点M、N、K.求证:DM•KE=DN•KF.
如图,△ABC的内切圆I切AB、BC、AC于点D、E、F.直线EF与AI、BI、DI交于点M、N、K.求证:DM•KE=DN•KF.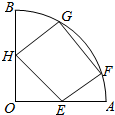 如图,四边形EFGH是圆心角为60°,半径为R的扇形的内接矩形,点F,G在$\widehat{AB}$上,求四边形EFGH的最大面积.
如图,四边形EFGH是圆心角为60°,半径为R的扇形的内接矩形,点F,G在$\widehat{AB}$上,求四边形EFGH的最大面积.