题目内容
11.直线l1:2x+(m+1)y+4=0和直线l2:mx+3y-2=0平行,则m=( )| A. | -3或2 | B. | 2 | C. | -2或3 | D. | 3 |
分析 利用直线l1:2x+(m+1)y+4=0和直线l2:mx+3y-2=0平行,$\frac{2}{m}=\frac{m+1}{3}≠\frac{4}{-2}$,即可求出m的值.
解答 解:∵直线l1:2x+(m+1)y+4=0和直线l2:mx+3y-2=0平行,
∴$\frac{2}{m}=\frac{m+1}{3}≠\frac{4}{-2}$,
解得:m=-3或2.
故选:A.
点评 本题考查直线的一般式方程与直线的平行关系,考查解方程的能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
2.在我国明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(加增的顺序为从塔顶到塔底).答案应为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
16.已知椭圆:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<3),左右焦点分别为F1,F2,过F1的直线l交椭圆于A、B两点,若|BF2|+|AF2|的最大值为10,则b的值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
1.已知θ为锐角,且sinθ=$\frac{3}{5}$,则sin(θ+45°)=( )
| A. | $\frac{7\sqrt{2}}{10}$ | B. | -$\frac{7\sqrt{2}}{10}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | -$\frac{\sqrt{2}}{10}$ |
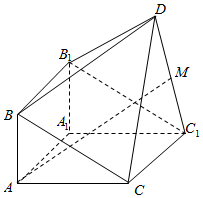 如图,由直三棱柱ABC-A1B1C1和四棱锥D-BB1C1C构成的几何体中,∠BAC=90°,AB=1,BC=BB1=2,C1D=CD=$\sqrt{5}$,平面CC1D⊥平面ACC1A1.
如图,由直三棱柱ABC-A1B1C1和四棱锥D-BB1C1C构成的几何体中,∠BAC=90°,AB=1,BC=BB1=2,C1D=CD=$\sqrt{5}$,平面CC1D⊥平面ACC1A1.