题目内容
17.已知函数f(x)=ax-lnx,g(x)=ln(x2-2x+a),(1)若a=0,求F(x)=f(x)+g(x)的零点;
(2)设命题P:f(x)在[$\frac{1}{4}$,$\frac{1}{2}$]单调递减,q:g(x)的定义域为R,若p∧q为真命题,求a的范围.
分析 (1)令F(x)=0,求出函数的零点即可;
(2)关于p:求出函数的导数,$a-\frac{1}{x}≤0$在$[{\frac{1}{4},\frac{1}{2}}]$恒成立,求出a的范围,关于q:根据二次函数的性质求出a的范围,取交集即可.
解答 解(1)∵a=0,∴F(x)=ln(x2-2x)-lnx,
由F(x)=0得x2-2x=x,∴x=0或x=3,
又因为F(x)的定义域{x|x>2},
∴x=0舍去,
∴F(x)的零点为3;
(2)∵${f^'}(x)=a-\frac{1}{x},且f(x)在[{\frac{1}{4},\frac{1}{2}}]$递减,
∴$a-\frac{1}{x}≤0$在$[{\frac{1}{4},\frac{1}{2}}]$恒成立,
∴a≤2,
又因为g(x)的定义域为R,
所以x2-2x+a>0对一切实数恒成立,
∴4-4a<0,∴a>1,
∵p∧q为真,
∴1<a≤2.
点评 本题考查了函数的零点问题,考查函数恒成立问题以及二次函数的性质,是一道中档题.

练习册系列答案
相关题目
14.为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图,记成绩不低于70分者为“成绩优良”.
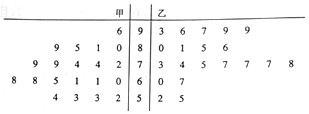
(1)分别计算甲、乙两班20个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
佳;
(2)甲、乙两班40个样本中,成绩在60分以下的学生中任意选取2人,求这2人来自不同班级的概率;
(3)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)},(n=a+b+c+d)$
独立性检验临界值表:

(1)分别计算甲、乙两班20个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
佳;
(2)甲、乙两班40个样本中,成绩在60分以下的学生中任意选取2人,求这2人来自不同班级的概率;
(3)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
独立性检验临界值表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
9.已知直线l1:y=ax-2a+5过定点A,则点A到直线l:x-2y+3=0的距离为( )
| A. | $2\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
6.某地震观测站对地下水位的变化和发生地震的情况共进行了n=1 700次观测,列联表如下:
问观测结果是否说明地下水位的变化与地震的发生相关?
| Y X | 有震 | 无震 | 合计 |
| 水位有变化 | 100 | 900 | 1 000 |
| 水位无变化 | 80 | 620 | 7 00 |
| 合计 | 180 | 1520 | 1700 |
| P(X2≥x0) | 0.15 | 0.1 | 0.05 |
| x0 | 2.072 | 2.706 | 3.841 |
