题目内容
14.为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图,记成绩不低于70分者为“成绩优良”.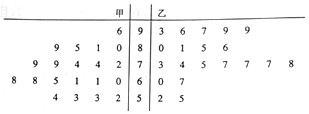
(1)分别计算甲、乙两班20个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
佳;
(2)甲、乙两班40个样本中,成绩在60分以下的学生中任意选取2人,求这2人来自不同班级的概率;
(3)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
独立性检验临界值表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
分析 (1)根据茎叶图计算甲、乙两班化学成绩前10名学生的平均分即可;
(2)确定基本事件的个数,即可求出这2人来自不同班级的概率;
(3)填写列联表,计算K2,对照数表即可得出结论.
解答 解:(1)甲班样本化学成绩前十的平均分为$\overline{x_甲}=\frac{1}{10}(72+74+74+79+79+80+81+85+89+96)=80.9$;
乙班样本化学成绩前十的平均分为$\overline{x_乙}=\frac{1}{10}(78+80+81+85+86+93+96+97+99+99)=89.4$;
甲班样本化学成绩前十的平均分远低于乙班样本化学成绩前十的平均分,大致可以判断“高效课堂”教学方式的教学效果更佳.
(2)样本中成绩6(0分)以下的学生中甲班有4人,记为:a,b,c,d,乙班有2人,记为:1,2.
则从a,b,c,d,1,2六个元素中任意选2个的所有基本事件如下:ab,ac,ad,a1,a2,bc,bd,b1,b2,cd,c1,c2,d1,d2,12,一共有15个基本事件,
设A表示“这2人来自不同班级”有如下:a1,a2,b1,b2,c1,c2,d1,d2,一共有8个基本事件,
所以$P(A)=\frac{8}{15}$.
(3)
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
∴能在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”.
点评 本题考查了计算平均数与独立性检验的应用问题,考查概率的计算,解题时应根据列联表求出观测值,对照临界值表得出结论,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知F是抛物线C:y=2x2的焦点,点P(x,y)在抛物线C上,且x=1,则|PF|=( )
| A. | $\frac{9}{8}$ | B. | $\frac{3}{2}$ | C. | $\frac{17}{8}$ | D. | $\frac{5}{2}$ |
19.如表,将数字1,2,3,…,2n(n≥3)全部填入一个2行n列的表格中,每格填一个数字.第一行填入的数字依次为a1,a2,…,an,第二行填入的数字依次为b1,b2,…,bn.
记${S_n}=\sum_{i=1}^n{|{a_i}-{b_i}|}=\;|{a_1}-{b_1}|+|{a_2}-{b_2}|+…+|{a_n}-{b_n}|$.
(Ⅰ)当n=3时,若a1=1,a2=3,a3=5,写出S3的所有可能的取值;
(Ⅱ)给定正整数n.试给出a1,a2,…,an的一组取值,使得无论b1,b2,…,bn填写的顺序如何,Sn都只有一个取值,并求出此时Sn的值;
(Ⅲ)求证:对于给定的n以及满足条件的所有填法,Sn的所有取值的奇偶性相同.
记${S_n}=\sum_{i=1}^n{|{a_i}-{b_i}|}=\;|{a_1}-{b_1}|+|{a_2}-{b_2}|+…+|{a_n}-{b_n}|$.
| a1 | a2 | … | an |
| b1 | b2 | … | bn |
(Ⅱ)给定正整数n.试给出a1,a2,…,an的一组取值,使得无论b1,b2,…,bn填写的顺序如何,Sn都只有一个取值,并求出此时Sn的值;
(Ⅲ)求证:对于给定的n以及满足条件的所有填法,Sn的所有取值的奇偶性相同.
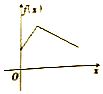
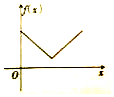
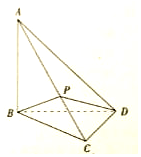 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )
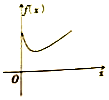
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )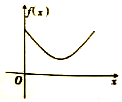
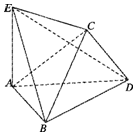 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.