题目内容
13.已知一组数据(2,3),(4,6),(6,9),(x0,y0)的线性回归方程为$\stackrel{∧}{y}$=x+2,则x0-y0的值为( )| A. | 2 | B. | 4 | C. | -4 | D. | -2 |
分析 利用平均数公式计算预报中心点的坐标,根据回归直线必过样本的中心点可得答案.
解答 解:由题意知$\overline{x}$=$\frac{1}{4}$(12+x0),$\overline{y}$=$\frac{1}{4}$(18+y0),
∵线性回归方程为$\stackrel{∧}{y}$=x+2,
∴$\frac{1}{4}$(18+y0)=$\frac{1}{4}$(12+x0)+2,
解得:x0-y0=-2,
故选:D.
点评 本题考查了线性回归直线的性质,回归直线必过样本的中心点.

练习册系列答案
相关题目
3.若$α∈(\frac{π}{2},π)$,且$3cos2α=sin(\frac{π}{4}-α)$,则cos2α的值为( )
| A. | $-\frac{{\sqrt{35}}}{18}$ | B. | $\frac{{\sqrt{35}}}{18}$ | C. | $\frac{17}{18}$ | D. | $-\frac{17}{18}$ |
1.某篮球运动员在最近5场比赛中所得分数分别为12,a,8,15,23,其中a>0,若该运动员在这5场比赛中得分的中位数为12,则得分的平均数不可能为( )
| A. | $\frac{68}{5}$ | B. | $\frac{69}{5}$ | C. | $\frac{71}{5}$ | D. | 14 |
8.某几何体的三视图如图所示,则该几何体的体积是( )
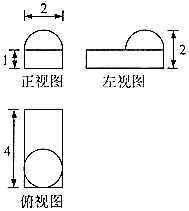

| A. | 8+$\frac{4}{3}$π | B. | 8+$\frac{2}{3}$π | C. | 4+$\frac{4π}{3}$ | D. | 4+$\frac{2π}{3}$ |
18.设正三棱锥A-BCD内接于球O,BC=1,E为AB的中点,AC⊥DE,则球的半径为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{10}}}{4}$ |
2.已知F是抛物线C:y=2x2的焦点,点P(x,y)在抛物线C上,且x=1,则|PF|=( )
| A. | $\frac{9}{8}$ | B. | $\frac{3}{2}$ | C. | $\frac{17}{8}$ | D. | $\frac{5}{2}$ |
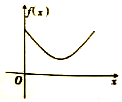
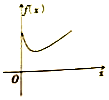
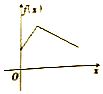
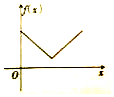
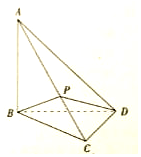 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )