题目内容
15．已知平面向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（3，1），则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为45°．分析 利用cos＜$\overrightarrow{a}，\overrightarrow{b}$＞=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$，能求出向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角．
解答 解：∵平面向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（3，1），
∴cos＜$\overrightarrow{a}，\overrightarrow{b}$＞=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{3+2}{\sqrt{5}•\sqrt{10}}$=$\frac{\sqrt{2}}{2}$，
∴＜$\overrightarrow{a}，\overrightarrow{b}$＞=45°．
∴向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角45°．
故答案为：45o．
点评 本题考查两向量的夹角的求法，是基础题，解题时要认真审题，注意平面向量坐标运算法则的合理运用．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
10．已知向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$，满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0，已知$\overrightarrow{a}$、$\overrightarrow{b}$成60°角，且$\overrightarrow{a}$、$\overrightarrow{b}$的大小分别为2和4，则$\overrightarrow{c}$的大小为（ ）
| A． | 6 | B． | 2 | C． | 2$\sqrt{5}$ | D． | 2$\sqrt{7}$ |
20．某地农业监测部门统计发现：该地区近几年的生猪收购价格每四个月会重复出现，但生猪养殖成本逐月递增．下表是今年前四个月的统计情况：
现打算从以下两个函数模型：
①y=Asin（ωx+φ）+B，（A＞0，ω＞0，-π＜φ＜π），
②y=log2（x+a）+b
中选择适当的函数模型，分别来拟合今年生猪收购价格（元/斤）与相应月份之间的函数关系、养殖成本（元/斤）与相应月份之间的函数关系．
（1）请你选择适当的函数模型，分别求出这两个函数解析式；
（2）按照你选定的函数模型，帮助该部门分析一下，今年该地区生猪养殖户在8月和9月有没有可能亏损？
| 月份 | 1月份 | 2月份 | 3月份 | 4月份 |
| 收购价格（元/斤） | 6 | 7 | 6 | 5 |
| 养殖成本（元/斤） | 3 | 4 | 4.6 | 5 |
①y=Asin（ωx+φ）+B，（A＞0，ω＞0，-π＜φ＜π），
②y=log2（x+a）+b
中选择适当的函数模型，分别来拟合今年生猪收购价格（元/斤）与相应月份之间的函数关系、养殖成本（元/斤）与相应月份之间的函数关系．
（1）请你选择适当的函数模型，分别求出这两个函数解析式；
（2）按照你选定的函数模型，帮助该部门分析一下，今年该地区生猪养殖户在8月和9月有没有可能亏损？
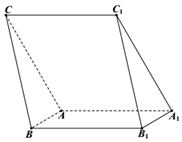如图，三棱柱ABC-A1B1C1中，侧面ACC1A1⊥侧面ABB1A1，∠B1A1A=∠C1A1A=60°，AA1=AC=4，AB=1．