题目内容
已知某个几何体的三视图如图所示,根据图中标出的尺寸,则这个几何体的体积是 .


考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由三视图想象出空间几何体,代入数据求体积即可.
解答:
解:由三视图可知,
这个几何体是由一个三棱柱截去了一个三棱锥,
其中三棱柱的体积V1=
×3×4×5=30,
三棱锥的体积V2=
×
×3×4×3=6.
故这个几何体的体积V=30-6=24
故答案为24.
这个几何体是由一个三棱柱截去了一个三棱锥,
其中三棱柱的体积V1=
| 1 |
| 2 |
三棱锥的体积V2=
| 1 |
| 3 |
| 1 |
| 2 |
故这个几何体的体积V=30-6=24
故答案为24.
点评:本题考查了学生的空间想象力,属于基础题.

练习册系列答案
相关题目
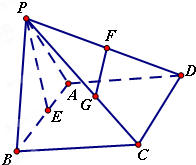 如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,△PAB是等边三角形,E、F、G分别是AB、PD、PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,△PAB是等边三角形,E、F、G分别是AB、PD、PC的中点.