题目内容
| 1-sin10 |
| A、cos5+sin5 |
| B、cos5-sin5 |
| C、sin5-cos5 |
| D、-sin5-cos5 |
考点：二倍角的正弦
专题：三角函数的求值
分析：直接利用二倍角公式以及同角三角函数的基本关系式化简求解即可．
解答：
解：
=
=|cos5-sin5|，
∵
＜5＜
，
∴cos5＞0＞sin5．
∴
=cos5-sin5．
故选：B．
| 1-sin10 |
| 1-2sin5cos5 |
∵
| 3π |
| 2 |
| 7π |
| 4 |
∴cos5＞0＞sin5．
∴
| 1-sin10 |
故选：B．
点评：本题考查二倍角公式的应用，三角函数的化简求值，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
已知复数z1=-
+
i，z2=-
-
i，则下列命题中错误的是（ ）
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| A、z12=z2 |
| B、|z1|=|z2| |
| C、z13-z23=1 |
| D、zl、z2互为共轭复数 |
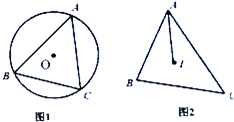在锐角△ABC中，BC=5，sinA=