题目内容
在△ABC中,D在BC边上,满足BD=2DC,cos∠BAD=
,cos∠CAD=
,AD=3,则AB= .
2
| ||
| 5 |
3
| ||
| 10 |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:如图,作BE∥AC交AD延长线于E点,则△ACD∽△EBD,相似比为2,易得DE=2AD,故AE=9,在三角形ABE中,利用锐角三角函数定义求出cos∠BAE与cosE的值,进而求出sin∠BAE与sin∠E,利用两角和与差的正弦函数公式化简sin∠ABE=sin(∠BAE+∠E),求出sin∠ABE的值,再利用正弦定理即可求出AB的长.
解答:
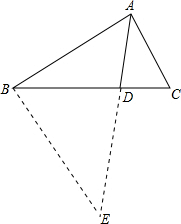 解:如图,作BE∥AC交AD延长线于E点,则△ACD∽△EBD,相似比为2,
解:如图,作BE∥AC交AD延长线于E点,则△ACD∽△EBD,相似比为2,
易得DE=2AD,故AE=9,
在△ABE中,cos∠BAE=
,cos∠E=cos∠CAD=
,
则sin∠BAE=
,sin∠E=
,
∴sin∠ABE=sin(∠BAE+∠E)=sin∠BAEcos∠E+cos∠BAEsin∠E=
×
+
×
=
,
由正弦定理得:
=
,即AB=
=
=
.
故答案为:
 解:如图,作BE∥AC交AD延长线于E点,则△ACD∽△EBD,相似比为2,
解:如图,作BE∥AC交AD延长线于E点,则△ACD∽△EBD,相似比为2,易得DE=2AD,故AE=9,
在△ABE中,cos∠BAE=
2
| ||
| 5 |
3
| ||
| 10 |
则sin∠BAE=
| ||
| 5 |
| ||
| 10 |
∴sin∠ABE=sin(∠BAE+∠E)=sin∠BAEcos∠E+cos∠BAEsin∠E=
| ||
| 5 |
3
| ||
| 10 |
2
| ||
| 5 |
| ||
| 10 |
| ||
| 2 |
由正弦定理得:
| AB |
| sin∠E |
| AE |
| sin∠ABE |
| AEsin∠E |
| sin∠ABE |
9×
| ||||
|
9
| ||
| 5 |
故答案为:
9
| ||
| 5 |
点评:此题考查了正弦、余弦定理,同角三角函数间的基本关系,熟练掌握定理是解本题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
如图所示的程序框图,若执行运算1×
×
×
×
,则在空白执行框中,应该填入( )
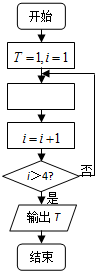
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |

| A、T=T•(i+1) | ||
| B、T=T•i | ||
C、T=T•
| ||
D、T=T•
|
