题目内容
在极坐标系中,直线l的方程为ρcosθ=5,则点(4,
)到直线l的距离为 .
| π |
| 3 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把极坐标化为直角坐标,即可得出.
解答:
解:直线l的方程为ρcosθ=5,化为x=5.
点(4,
)化为(2,2
).
∴点到直线l的距离d=5-2=3.
故答案为:3.
点(4,
| π |
| 3 |
| 3 |
∴点到直线l的距离d=5-2=3.
故答案为:3.
点评:本题考查了极坐标化为直角坐标、点到直线的距离,属于基础题.

练习册系列答案
相关题目
在空间中,α,β表示平面,m表示直线,已知α∩β=l,则下列命题正确的是( )
| A、若m∥l,则m与α,β都平行 |
| B、若m与α,β都平行,则m∥l |
| C、若m与l异面,则m与α,β都相交 |
| D、若m与α,β都相交,则m与l异面 |

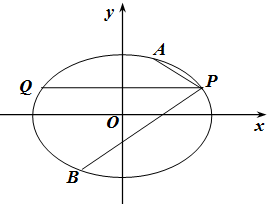 已知椭圆C的中心在原点,焦点在x轴上,离心率为
已知椭圆C的中心在原点,焦点在x轴上,离心率为