Question

已知椭圆C的中心在原点，焦点在x轴上，离心率为

3

2

，且经过点P（4，1）．
（Ⅰ）求椭圆C的方程；
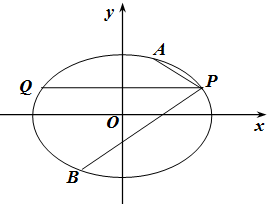
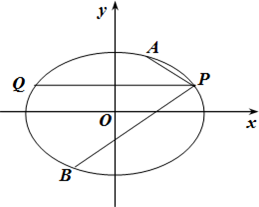
（Ⅱ）过点P的直线l：y=1与椭圆的另一个交点为Q，点A、B是椭圆C上位于直线l两侧的动点，且直线AP与BP关于l对称，求四边形APBQ面积的最大值．

Answer 1

考点：直线与圆锥曲线的综合问题,椭圆的标准方程,椭圆的简单性质,直线与圆锥曲线的关系

专题：圆锥曲线的定义、性质与方程

分析：（Ⅰ）设出标准方程，利用离心率以及椭圆经过的点，列出方程组，求出ab，即可求椭圆C的方程；
（Ⅱ）设直线AP的斜率为k，则直线BP的斜率为-k，A（x₁，y₁），B（x₂，y₂）．推出直线AP的方程为y=k（x-4）+1与椭圆方程联立，求出A、B的坐标，表示出四边形APBQ的面积，利用基本不等式求出四边形APBQ面积的最大值．

解答：
解：（Ⅰ）设所求椭圆的标准方程为

x2

a2

+

y2

b2

=1，焦距为2c…（1分）
由条件可得：e2=1-

b2

a2

=(

3

2

)2=

3

4

，∴a²=4b²，

16

a2

+

1

b2

=1，又a²=b²+c²
解得：a²=20，b²=5，故所求椭圆的标准方程为

x2

20

+

y2

5

=1…（5分）
（Ⅱ）设直线AP的斜率为k，则直线BP的斜率为-k，A（x₁，y₁），B（x₂，y₂）．
∴直线AP的方程为y=k（x-4）+1…（7分）
联立

x2 20 + y2 5 =1 y=k(x-4)+1

整理得（4k²+1）x²+（8k-32k²）x+64k²-32k-16=0．
∴x1+4=

32k2-8k

4k2+1

，x1=

16k2-8k-4

4k2+1

，∴y1=

-4k2-8k+1

4k2+1

…（9分）
将上式中的k用-k代入可得y2=

-4k2+8k+1

4k2+1

…（10分）
所以四边形APBQ的面积S=

1

2

|PQ|•|y2-y1|…（11分）
=

64|k|

4k2+1

=

64

4|k|+ 1 |k|

≤16…（12分）
故四边形APBQ面积的最大值为16…（13分）

点评：本题考查椭圆的标准方程的求法，直线与椭圆的位置关系的应用，基本不等式的应用，考查分析问题解决问题的能力．