题目内容
圆O1：x2+y2+2x-2y=0和圆O2：x2+y2-4x+6y-3=0的位置关系是（ ）
| A、相离 | B、相交 | C、内切 | D、外切 |
考点：圆与圆的位置关系及其判定
专题：计算题,直线与圆
分析：将圆的方程化为标准方程，求出两圆圆心距，即可得出结论．
解答：
解：圆O1：x2+y2+2x-2y=0可化为：（x+1）2+（y-1）2=2，圆心为（-1，1），半径为
圆O2：x2+y2-4x+6y-3=0可化为：（x-2）2+（y+3）2=16，圆心为（2，-3），半径为4，
∵两圆圆心距为
=5，
∴4-
＜5＜4+
，
∴圆O1：x2+y2+2x-2y=0和圆O2：x2+y2-4x+6y-3=0的位置关系是相交，
故选：B．
| 2 |
圆O2：x2+y2-4x+6y-3=0可化为：（x-2）2+（y+3）2=16，圆心为（2，-3），半径为4，
∵两圆圆心距为
| 32+42 |
∴4-
| 2 |
| 2 |
∴圆O1：x2+y2+2x-2y=0和圆O2：x2+y2-4x+6y-3=0的位置关系是相交，
故选：B．
点评：本题考查圆与圆的位置关系及其判定，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
若α的终边经过点P（3，-4），则tan（α+
）=（ ）
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
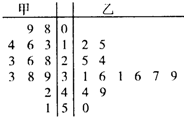某化肥厂甲、乙两个车间包装肥料，在自动包装传送带上每隔30min抽取一包产品，称其重量，用茎叶图分别记录抽查数据如下：