题目内容
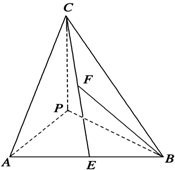 如图,四面体P-ABC中,PA、PB、PC两两垂直,PA=PB=2,PC=4,E是AB的中点,F是CE的中点.
如图,四面体P-ABC中,PA、PB、PC两两垂直,PA=PB=2,PC=4,E是AB的中点,F是CE的中点.(1)建立适当的直角坐标系,写出点B、C、E、F的坐标;
(2)求EF与底面ABP所成角的余弦值.
考点:直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)如图,以PA所在直线为x轴,PB所在直线为y轴,PC所在直线为z轴,P为原点建立直角坐标系,可得点B、C、E、F的坐标;
(2)证明∠FBG为BF与平面ABP所成的角,即可求EF与底面ABP所成角的余弦值.
(2)证明∠FBG为BF与平面ABP所成的角,即可求EF与底面ABP所成角的余弦值.
解答:
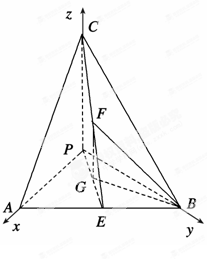 解:(1)如图,以PA所在直线为x轴,PB所在直线为y轴,PC所在直线为z轴,P为原点建立直角坐标系,则B点坐标为(0,2,0),C点坐标为(0,0,4),A点坐标为(2,0,0).
解:(1)如图,以PA所在直线为x轴,PB所在直线为y轴,PC所在直线为z轴,P为原点建立直角坐标系,则B点坐标为(0,2,0),C点坐标为(0,0,4),A点坐标为(2,0,0).
因为E为AB中点,所以E(1,1,0).
因为F为CE中点,所以F(
,
,2).
(2)连接PE,设G为PE中点,连接FG、BG,则G(
,
,0)
因为PA、PB、PC两两互相垂直,所以PC⊥平面ABP,
因为F、G分别为CE、PE的中点,
所以FG∥PC,所以FG⊥面ABP.
故∠FEG为EF与平面ABP所成的角.
因为
=(-
,-
,2),
=(-
,-
,0).
所以cos∠FEG=
=
,
即EF与底面ABP所成的角的余弦值为
.
 解:(1)如图,以PA所在直线为x轴,PB所在直线为y轴,PC所在直线为z轴,P为原点建立直角坐标系,则B点坐标为(0,2,0),C点坐标为(0,0,4),A点坐标为(2,0,0).
解:(1)如图,以PA所在直线为x轴,PB所在直线为y轴,PC所在直线为z轴,P为原点建立直角坐标系,则B点坐标为(0,2,0),C点坐标为(0,0,4),A点坐标为(2,0,0).因为E为AB中点,所以E(1,1,0).
因为F为CE中点,所以F(
| 1 |
| 2 |
| 1 |
| 2 |
(2)连接PE,设G为PE中点,连接FG、BG,则G(
| 1 |
| 2 |
| 1 |
| 2 |
因为PA、PB、PC两两互相垂直,所以PC⊥平面ABP,
因为F、G分别为CE、PE的中点,
所以FG∥PC,所以FG⊥面ABP.
故∠FEG为EF与平面ABP所成的角.
因为
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| EG |
| 1 |
| 2 |
| 1 |
| 2 |
所以cos∠FEG=
| ||||||||
|
| 1 |
| 3 |
即EF与底面ABP所成的角的余弦值为
| 1 |
| 3 |
点评:本题考查BF与底面ABP所成的角的余弦值,考查向量知识的运用,正确求出向量的坐标是关键.

练习册系列答案
相关题目
设8(a3-1)=(a-1)(a+1)(a2+a+1),且a≠1,则a的值是( )
| A、7 | B、15 | C、35 | D、63 |
函数f(x)=|x|与g(x)=x(2-x)的单调增区间依次为( )
| A、(-∞,0],[1,+∞) |
| B、(-∞,0],(-∞,1] |
| C、[0,+∞),[1,+∞) |
| D、[0,+∞),(-∞,1] |
如图是正方体的表面展开图,则下列描述正确的是( )


| A、BM与ED平行 |
| B、CN与BM相交 |
| C、CN与BE异面 |
| D、DM与AF平行 |
