题目内容
13.在直角坐标系xOy中,直线l的参数方程为 $\left\{\begin{array}{l}x=1+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$.(t为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=acosθ,(a>0)(Ⅰ) 求直线l和曲线C的普通方程;
(Ⅱ) 若直线l与曲线C相切,求a的值.
分析 (I)消参数得到直线l的普通方程,对ρ=acosθ两边平方得出曲线C的普通方程;
(II)根据直线与圆相切得出圆心到直线的距离等于半径,列方程解出a.
解答 解:(I)∵$\left\{\begin{array}{l}x=1+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$,∴x=1+y,即x-y-1=0.∴直线l的普通方程为x-y-1=0.
∵ρ=acosθ,∴ρ2=aρcosθ,∴曲线C的普通方程为x2+y2-ax=0.即(x-$\frac{a}{2}$)2+y2=$\frac{{a}^{2}}{4}$.
(II)由(1)知曲线C的圆心为($\frac{a}{2}$,0),半径为$\frac{a}{2}$.
∵直线l与曲线C相切,∴$\frac{|\frac{a}{2}-1|}{\sqrt{2}}=\frac{a}{2}$,解得a=2$\sqrt{2}$-2.
点评 本题考查了参数方程,极坐标方程与普通方程的转化,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
5.函数y=log${\;}_{\frac{1}{3}}$(x2-ax+3)在[1,2]上恒为正数,则a的取值范围是( )
| A. | 2$\sqrt{2}$<a<2$\sqrt{3}$ | B. | 2$\sqrt{2}$<a<$\frac{7}{2}$ | C. | 3<a<$\frac{7}{2}$ | D. | 3<a<2$\sqrt{3}$ |
3.函数f(x)=x2-x-1的零点有( )
| A. | 2个 | B. | 1个 | C. | 0个 | D. | 都有可能 |
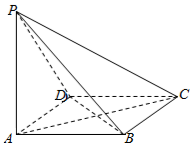 如图,四棱锥P-ABCD的底面为菱形,且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=$\sqrt{3}$.
如图,四棱锥P-ABCD的底面为菱形,且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=$\sqrt{3}$.