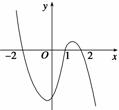
题目内容
设函数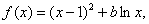 其中b为常数.
其中b为常数.
(1)当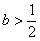 时,判断函数
时,判断函数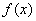 在定义域上的单调性;
在定义域上的单调性;
(2)若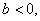 求
求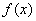 的极值点;
的极值点;
(3)求证对任意不小于3的正整数n,不等式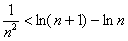 都成立.
都成立.
解:(1)由题意知,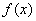 的定义域为
的定义域为

∴当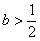 时,
时, ,函数
,函数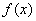 在定义域
在定义域 上单调递增.
上单调递增.
(2) 时,
时, 有两个不同解,
有两个不同解,

 舍去,而
舍去,而
此时 随x在定义域上的变化情况如下表:(表略)
随x在定义域上的变化情况如下表:(表略)
由此表可知: 时,
时,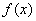 有惟一极小值点,
有惟一极小值点,
(3)由(2)可知当 时,函数
时,函数
此时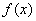 有惟一极小值点
有惟一极小值点 且
且 时,
时,

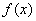 在
在 为减函数
为减函数
∴当 时,
时,
∴恒有 即恒有
即恒有
∴当 时,恒有
时,恒有 成立
成立

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 。
。 处的切线方程; (2)求该切线与坐标轴所围成的三角形面积。
处的切线方程; (2)求该切线与坐标轴所围成的三角形面积。 中,
中, 则
则 ( )
( )  B.
B. C.
C. D.
D.
 的解集是R,则实数m的取值范围是__ __.
的解集是R,则实数m的取值范围是__ __.

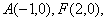 定直线
定直线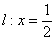 ,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N.
,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N. 则p,q的大小关系是( )
则p,q的大小关系是( )