题目内容
已知定点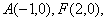 定直线
定直线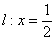 ,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N.
,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N.
(1)求E的方程;
(2)试判断以线段MN为直径的圆是否过点F,并说明理由.
解:(1)设 则
则 化简得
化简得
(2)①当直线BC与x轴不垂直时,
设BC的方程为 与双曲线
与双曲线 联立消去y得
联立消去y得
 ,由题意知
,由题意知 且
且
设 则
则 ,
,



因为 所以直线AB的方程为
所以直线AB的方程为
因此M点的坐标为

同理可得
因此

②当直线BC与x轴垂直时,方程为 则
则
AB的方程为 因此M点的坐标为
因此M点的坐标为

同理可得 因此
因此
综上 即
即
故以线段MN为直径的圆经过点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 时,△ABC的面积为________.
时,△ABC的面积为________.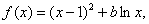 其中b为常数.
其中b为常数.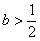 时,判断函数
时,判断函数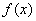 在定义域上的单调性;
在定义域上的单调性;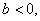 求
求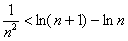 都成立.
都成立. 和曲线
和曲线 所围成的图形的面积为________.
所围成的图形的面积为________.

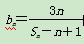 的前n项和为Tn,证明:Tn<6.
的前n项和为Tn,证明:Tn<6. 的前100项和为( )
的前100项和为( ) B.
B. C.
C. D.
D.
 A.
A. B.
B.
 D.
D.