题目内容
已知函数f(x)=x2-2a2lnx(a>0).
(Ⅰ)若f(x)在x=1处取得极值,求实数a的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若f(x)在[1,e]上没有零点,求实数a的取值范围.
(Ⅰ)若f(x)在x=1处取得极值,求实数a的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若f(x)在[1,e]上没有零点,求实数a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:压轴题
分析:(Ⅰ)利用极值点的导函数为零,求出参数的值,再通过单调性验证参数适合题意;
(Ⅱ)利用导函数值的正负求出函数的单调区间;
(Ⅲ)利用导函数值研究函数的单调性和极值,必须讨论极值点与区间的位置关系.
(Ⅱ)利用导函数值的正负求出函数的单调区间;
(Ⅲ)利用导函数值研究函数的单调性和极值,必须讨论极值点与区间的位置关系.
解答:
解:(Ⅰ)f(x)=x2-2a2lnx(a>0)的定义域为(0,+∞).
f ′(x)=2x-
=
=
,
∵f(x)在x=1处取得极值,
∴f′(1)=0,解得a=1或a=-1(舍).
∴a=1.
当a=1时,x∈(0,1),f′(x)<0;
x∈(1,+∞),f′(x)>0,
所以a的值为1.
(Ⅱ)令f′(x)=0,解得x=a或x=-a(舍).
当x在(0,+∞)内变化时,f′(x),f(x)的变化情况如下:
由上表知f(x)的单调递增区间为(a,+∞),单调递减区间为(0,a).
(Ⅲ)要使f(x)在[1,e]上没有零点,只需在[1,e]上f(x)min>0或f(x)max<0,
又f(1)=1>0,只须在区间[1,e]上f(x)min>0.
(1)当a≥e时,f(x)在区间[1,e]上单调递减,f(x)min=f(e)=e2-2a2>0,
解得 0<a<
与a≥e矛盾.
(2)当1<a<e时,f(x)在区间[1,a)上单调递减,在区间(a,e]上单调递增,
f(x)min=f(a)=a2(1-2lna)>0,解得0<a<
,
所以1<a<
.
(3)当0<a≤1时,f(x)在区间[1,e]上单调递增,f(x)min=f(1)>0,满足题意.
综上,a的取值范围为:0<a<
.
f ′(x)=2x-
| 2a2 |
| x |
| 2x2-2a2 |
| x |
| 2(x+a)(x-a) |
| x |
∵f(x)在x=1处取得极值,
∴f′(1)=0,解得a=1或a=-1(舍).
∴a=1.
当a=1时,x∈(0,1),f′(x)<0;
x∈(1,+∞),f′(x)>0,
所以a的值为1.
(Ⅱ)令f′(x)=0,解得x=a或x=-a(舍).
当x在(0,+∞)内变化时,f′(x),f(x)的变化情况如下:
| x | (0,a) | a | (a,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
(Ⅲ)要使f(x)在[1,e]上没有零点,只需在[1,e]上f(x)min>0或f(x)max<0,
又f(1)=1>0,只须在区间[1,e]上f(x)min>0.
(1)当a≥e时,f(x)在区间[1,e]上单调递减,f(x)min=f(e)=e2-2a2>0,
解得 0<a<
| ||
| 2 |
(2)当1<a<e时,f(x)在区间[1,a)上单调递减,在区间(a,e]上单调递增,
f(x)min=f(a)=a2(1-2lna)>0,解得0<a<
| e |
所以1<a<
| e |
(3)当0<a≤1时,f(x)在区间[1,e]上单调递增,f(x)min=f(1)>0,满足题意.
综上,a的取值范围为:0<a<
| e |
点评:本题考查的是导函数知识,包括导函数与单调性、导函数与极值,并利用极值研究方程的根,本题还考查了分类讨论的数学思想,考查了学生分析问题、解决问题的能力,属于难题.

练习册系列答案
相关题目
已知复数z满足z(1+i)=1(其中i为虚数单位),则z的共轭复数
是( )
. |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
执行如图的程序框图输出的T的值为( )


| A、4 | B、6 | C、8 | D、10 |
 为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.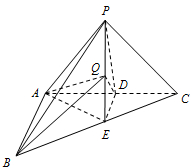 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2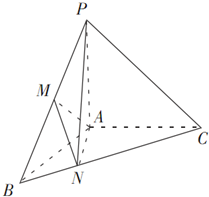 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.