题目内容
已知菱形ABCD的边长4,∠ABC=150°,若在菱形内任取一 点,则该点到菱形的四个顶点的距离均大于1的概率为 .
考点:几何概型
专题:概率与统计
分析:以菱形ABCD的各个顶点为圆心、半径为1作圆如图所示,可得当该点位于图中阴影部分区域时,它到四个顶点的距离均不小于1.因此算出菱形ABCD的面积和阴影部分区域的面积,利用几何概型计算公式加以计算,即可得到所求的概率.
解答:
解: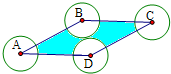 分别以菱形ABCD的各个顶点为圆心,作半径为1的圆,如图所示.
分别以菱形ABCD的各个顶点为圆心,作半径为1的圆,如图所示.
在菱形ABCD内任取一点P,则点P位于四个圆的外部或在圆上时,
满足点P到四个顶点的距离均不小于1,即图中的阴影部分区域
∵S菱形ABCD=AB•BCsin30°=4×4×
=8,
∴S阴影=S菱形ABCD-S空白=8-π×12=8-π.
因此,该点到四个顶点的距离均不小于1的概率P=
=
=1-
,
故答案为:1-
 分别以菱形ABCD的各个顶点为圆心,作半径为1的圆,如图所示.
分别以菱形ABCD的各个顶点为圆心,作半径为1的圆,如图所示.在菱形ABCD内任取一点P,则点P位于四个圆的外部或在圆上时,
满足点P到四个顶点的距离均不小于1,即图中的阴影部分区域
∵S菱形ABCD=AB•BCsin30°=4×4×
| 1 |
| 2 |
∴S阴影=S菱形ABCD-S空白=8-π×12=8-π.
因此,该点到四个顶点的距离均不小于1的概率P=
| S阴影 |
| SABCD |
| 8-π |
| 8 |
| π |
| 8 |
故答案为:1-
| π |
| 8 |
点评:本题给出菱形ABCD,求在菱形内部取点,使该点到各个顶点的距离均不小于1的概率.着重考查了菱形的面积公式、圆的面积公式和几何概型计算公式等知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=x3-x2+a在[-1,1]的最小值是1,则实数a的值是( )
| A、1 | ||
| B、3 | ||
C、
| ||
| D、-1 |