题目内容
如果等差数列{an}中，a3+a4+a5=12，那么a1+a2+a3+…+a7=（ ）
| A、35 | B、28 | C、21 | D、14 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：由等差数列的性质求解．
解答：
解：∵a3+a4+a5=3a4=12，∴a4=4，
∴a1+a2+…+a7=
（a1+a7）=7a4=28
故选B．
∴a1+a2+…+a7=
| 7 |
| 2 |
故选B．
点评：本题主要考查等差数列的性质．
练习册系列答案
相关题目
设P和Q是两个集合，定义集合P-Q={x|x∈P，且x∉Q}，如果P={x|log2x＜1}，{x||x-2|＜1}，那么P-Q=（ ）
| A、{x|0＜x＜1} |
| B、{x|x＜x≤1} |
| C、{x|1≤x＜2} |
| D、{x|2≤x＜3} |
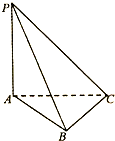如图，在三棱锥P-ABC中，已知△ABC是等腰直角三角形，∠ABC=90°，△PAC是直角三角形，∠PAC=90°，∠ACP=30°，平面PAC⊥平面ABC．
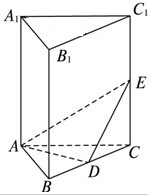已知在直三棱柱ABC-A1B1C1中，E为CC1上任意一点，D在BC上（点D不同于点C），AD⊥DE，求证：平面ADE⊥平面BCC1B1．