题目内容
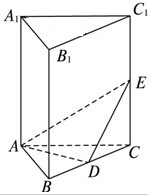已知在直三棱柱ABC-A1B1C1中，E为CC1上任意一点，D在BC上（点D不同于点C），AD⊥DE，求证：平面ADE⊥平面BCC1B1．考点：平面与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：依题意，可证AD⊥平面BCC1B1，再利用面面垂直的判定定理即可证得平面ADE⊥平面BCC1B1．
解答：
证明：因为ABC-A1B1C1是直三棱柱，所以CC1⊥平面ABC．
又AD?平面ABC，所以CC1⊥AD．
又因为AD⊥DE，CC1，DE?平面BCC1B1，CC1∩DE=E，
所以AD⊥平面BCC1B1．
又AD?平面ADE，所以平面ADE⊥平面BCC1B1．
又AD?平面ABC，所以CC1⊥AD．
又因为AD⊥DE，CC1，DE?平面BCC1B1，CC1∩DE=E，
所以AD⊥平面BCC1B1．
又AD?平面ADE，所以平面ADE⊥平面BCC1B1．
点评：本题考查平面与平面垂直的判定，考查分析与作图能力，属于中档题．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
在复平面上，复数z=
对应点所在的象限是（ ）
| 3+i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如果等差数列{an}中，a3+a4+a5=12，那么a1+a2+a3+…+a7=（ ）
| A、35 | B、28 | C、21 | D、14 |