题目内容
3.若a>0,b>0,且42a+b=2ab,则a+b的最小值是( )| A. | 12 | B. | 6+2$\sqrt{2}$ | C. | 6+4$\sqrt{2}$ | D. | 6+4$\sqrt{3}$ |
分析 a>0,b>0,且42a+b=2ab,即24a+2b=2ab,可得4a+2b=ab,化为:$\frac{4}{b}$+$\frac{2}{a}$=1.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵a>0,b>0,且42a+b=2ab,即24a+2b=2ab,可得4a+2b=ab,化为:$\frac{4}{b}$+$\frac{2}{a}$=1.
则a+b=(a+b)$(\frac{4}{b}+\frac{2}{a})$=2$(3+\frac{2a}{b}+\frac{b}{a})$≥2$(3+2\sqrt{\frac{2a}{b}×\frac{b}{a}})$=6+4$\sqrt{2}$,当且仅当b=$\sqrt{2}$a=4+2$\sqrt{2}$时取等号.
因此其最小值是6+4$\sqrt{2}$,
故选:B.
点评 本题考查了“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.中心在原点,对称轴为坐标轴的双曲线C与圆O:x2+y2=10有公共点P(3,-1),且圆O在P点处的切线与双曲线C的一条渐近线平行,则该双曲线的实轴长为( )
| A. | $\frac{4\sqrt{5}}{3}$ | B. | 4$\sqrt{5}$ | C. | $\frac{8\sqrt{5}}{3}$ | D. | 8$\sqrt{5}$ |
12.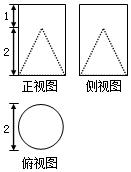 在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
 在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )| A. | (7+$\sqrt{5}$)π | B. | (7+2$\sqrt{5}$)π | C. | (8+$\sqrt{5}$)π | D. | (8+2$\sqrt{5}$)π |
13.若(ax+2)4展开式中含有x3项的系数为8则$\int_a^{e^2}{\frac{1}{x}dx=}$( )
| A. | .2 | B. | .$-\frac{1}{e^2}-1$ | C. | .$-\frac{1}{e^2}+1$ | D. | 2-e |