题目内容
10.函数$f(x)=\frac{3}{x-4}+\sqrt{{2^x}-4}$的定义域是( )| A. | [2,4) | B. | [2,4)∪(4,+∞) | C. | (2,4)∪(4,+∞) | D. | [2,+∞) |
分析 由根式内部的代数式大于等于0,分式的分母不为0联立不等式组求解.
解答 解:由$\left\{\begin{array}{l}{x-4≠0}\\{{2}^{x}-4≥0}\end{array}\right.$,解得x≥2且x≠4.
∴函数$f(x)=\frac{3}{x-4}+\sqrt{{2^x}-4}$的定义域是[2,4)∪(4,+∞).
故选:B.
点评 本题考查函数的定义域及其求法,是基础的计算题.

练习册系列答案
相关题目
20.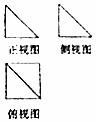 如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
 如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
2.已知单位圆有一条长为$\sqrt{2}$的弦AB,动点P在圆内,则使得$\overrightarrow{AP}$$•\overrightarrow{AB}$≥2的概率为( )
| A. | $\frac{π-2}{4π}$ | B. | $\frac{π-2}{π}$ | C. | $\frac{3π-2}{4π}$ | D. | $\frac{2}{π}$ |
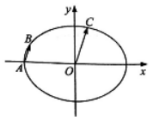 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2}{3}$,C为椭圆上位于第一象限内的一点.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2}{3}$,C为椭圆上位于第一象限内的一点.