题目内容
8.设函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≥0}\\{{x}^{2},x<0}\end{array}\right.$,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1,x2,则e${\;}^{{x}_{1}}$•e${\;}^{{x}_{2}}$的最大值为( )| A. | $\frac{1}{{e}^{2}}$ | B. | 2(ln2-1) | C. | $\frac{4}{{e}^{2}}$ | D. | ln2-1 |
分析 求出f(f(x))的解析式,根据f(f(x))的函数图象判断x1,x2的范围和两根的关系,构造函数h(x1)=e${\;}^{{x}_{1}}$•e${\;}^{{x}_{2}}$,求出h(x1)的最大值即可.
解答 解:令g(x)=f(f(x))=$\left\{\begin{array}{l}{{e}^{{e}^{x}},x≥0}\\{{e}^{{x}^{2}},x<0}\end{array}\right.$,
∵y=f(x)在(-∞,0)上单调递减,在[0,+∞)上单调递增,
∴g(x)=f(f(x))在(-∞,0)上单调递减,在[0,+∞)上单调递增.
做出g(x)=f(f(x))的函数图象如图所示: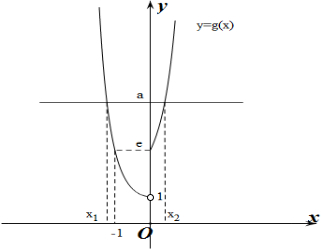
∵方程f(f(x))=a(a>0)恰有两个不相等的实根x1,x2,
不妨设x1<x2,则x1≤-1,x2≥0,且f(x1)=f(x2),即x12=e${\;}^{{x}_{2}}$.
∴e${\;}^{{x}_{1}}$•e${\;}^{{x}_{2}}$=e${\;}^{{x}_{1}}$•x12,
令h(x1)=e${\;}^{{x}_{1}}$•x12,则h′(x1)=e${\;}^{{x}_{1}}$(x12+2x1)=e${\;}^{{x}_{1}}$•x1•(x1+2),
∴当x1<-2时,h′(x1)>0,当-2<x1<-1时,h′(x1)<0,
∴h(x1)在(-∞,-2)上单调递增,在(-2,-1)上单调递减,
∴当x1=-2时,h(x1)取得最大值h(-2)=$\frac{4}{{e}^{2}}$.
故选C.
点评 本题考查了根的个数与函数图象的关系,函数单调性判断与函数最值的计算,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知O为坐标原点,F1、F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点,A为C的左顶点,P为C上一点,且PF1⊥x轴,过点A的直线l与线段PF1交于点M,与y轴交于点E,若直线F2M与y轴交点为N,OE=2ON,则C的离心率为( )
| A. | $\frac{1}{3}$ | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
19.已知集合A={x|x2+5x>0},B={x|-3<x<4},则A∩B等于( )
| A. | (-5,0) | B. | (-3,0) | C. | (0,4) | D. | (-5,4) |
3.执行如图所示的程序框图,若输出的结果是6,则判断框内m的取值范围是( )
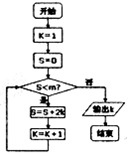

| A. | (30,42] | B. | (20,30) | C. | (20,30] | D. | (20,42) |
13.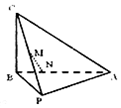 如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
(1)求AN的长;
(2)求锐二面角P-NC-A的余弦值.
 如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.(1)求AN的长;
(2)求锐二面角P-NC-A的余弦值.
20.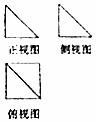 如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
 如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
17.已知函数$f(x)=\left\{\begin{array}{l}{e^x}+a,x≤0\\{x^2}+1+a.x>0\end{array}\right.$,a为实数,若f(2-x)≥f(x),则x的取值范围是( )
| A. | (-∞,1] | B. | (-∞,-1] | C. | [-1,+∞) | D. | [1,+∞) |