题目内容
7．抛物线y=ax2的准线方程是（ ）| A． | $y=-\frac{a}{2}$ | B． | $y=-\frac{a}{4}$ | C． | $y=-\frac{1}{2a}$ | D． | $y=-\frac{1}{4a}$ |
分析 将方程化为标准方程，再分类讨论，求出抛物线y=ax2的准线方程．
解答 解：首先将方程化为标准方程${x^2}=\frac{1}{a}y=2•\frac{1}{2a}y$．
当a＞0时，$y=-\frac{1}{4a}$；当a＜0时，$y=-\frac{1}{4a}$．
所以抛物线y=ax2的准线方程是 $y=-\frac{1}{4a}$．
故选D．
点评 本题考查求抛物线的准线方程，考查学生的计算能力，比较基础．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
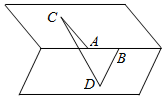如图，已知在一个二面角的棱上有两个点A、B，线段AC、BD分别在这个二面角的两个面内，并且都垂直于棱AB，AB=4cm，AC=6cm，BD=8cm，CD=2$\sqrt{17}$cm，则这个二面角的度数为60°．
