题目内容
17．若函数f（x）=2m（lnx+x）-x2有唯一零点，则m的取值范围是m＜0或m=$\frac{1}{2}$．分析 由f（x）=0得2m（lnx+x）=x2，根据函数与方程之间的关系转化为两个函数的交点问题，利用数形结合进行求解即可．
解答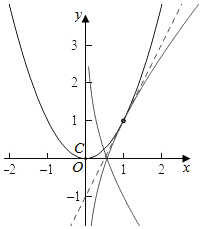 
解：由f（x）=2m（lnx+x）-x2=0，
得2m（lnx+x）=x2，
若m=0，则x=0，不满足函数的定义域（0，+∞），故m≠0，
设h（x）=2m（lnx+x），则函数的定义域为（0，+∞），
函数的导数h′（x）=2m（1+$\frac{1}{x}$），
若m＜0，则h′（x）＜0恒成立，则函数单调递减，此时函数h（x）与y=x2，在（0，+∞）上只有一个交点，满足条件．
若m＞0，则h′（x）＞0恒成立，则函数单调递增，
要使函数f（x）只有一个零点，则两个函数只有一个交点，即此时两个函数相切，
设切点为（a，b），
则h′（x）=2m（1+$\frac{1}{x}$），y′=2x，
则满足$\left\{\begin{array}{l}{2m（1+\frac{1}{a}）=2a}\\{2m（lna+a）={a}^{2}}\end{array}\right.$得a=1，m=$\frac{1}{2}$，
综上m＜0或m=$\frac{1}{2}$，
故答案为：m＜0或m=$\frac{1}{2}$．
点评 本题主要考查函数与方程的应用，利用转化法转化为两个函数的交点个数问题，借助导数和数形结合研究函数的单调性是解决本题的关键．
练习册系列答案
相关题目
7．抛物线y=ax2的准线方程是（ ）
| A． | $y=-\frac{a}{2}$ | B． | $y=-\frac{a}{4}$ | C． | $y=-\frac{1}{2a}$ | D． | $y=-\frac{1}{4a}$ |
9．设x1，x2（x1＜x2）是函数f（x）=lnx+$\frac{1}{2}$x2-（b-1）x的两个极值点，若b≥$\frac{7}{2}$，则$\frac{{x}_{1}}{{x}_{2}}$的最大值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{2}{3}$ |