题目内容
19．“方程$\frac{{x}^{2}}{2+n}$-$\frac{{y}^{2}}{n+1}$=1表示双曲线”是“n＞-1”的（ ）| A． | 充分不必要条件 | B． | 必要且不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 方程$\frac{{x}^{2}}{2+n}$-$\frac{{y}^{2}}{n+1}$=1表示双曲线?（2+n）（n+1）＞0，解得n即可得出．
解答 解：方程$\frac{{x}^{2}}{2+n}$-$\frac{{y}^{2}}{n+1}$=1表示双曲线?（2+n）（n+1）＞0，解得n＞-1或n＜-2．
∴“方程$\frac{{x}^{2}}{2+n}$-$\frac{{y}^{2}}{n+1}$=1表示双曲线”是“n＞-1”的必要不充分条件．
故选：B．
点评 本题考查了双曲线的标准、一元二次不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
9．
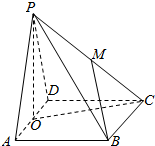已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，侧面PAD是边长为2的正三角形，平面ABCD⊥平面PAD，M是PC的中点，O是AD的中点，则直线BM与平面PCO所成角的正弦值是（ ）
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，侧面PAD是边长为2的正三角形，平面ABCD⊥平面PAD，M是PC的中点，O是AD的中点，则直线BM与平面PCO所成角的正弦值是（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{2\sqrt{5}}{5}$ | C． | $\frac{1}{5}$ | D． | $\frac{\sqrt{2}}{3}$ |
10．在8件获奖作品中，有3件一等奖，有5件二等奖，从这8件作品中任取3件．
（1）求取出的3件作品中，一等奖多于二等奖的概率；
（2）设X为取出的3件作品中一等奖的件数，求随机变量X的分布列和数学期望．
（1）求取出的3件作品中，一等奖多于二等奖的概率；
（2）设X为取出的3件作品中一等奖的件数，求随机变量X的分布列和数学期望．
7．某商场销售一种“艾丽莎”品牌服装，销售经理根据销售记录发现，该服装在过去的一个月内（以30天计）每件的销售价格P（x）（百元）与时间x（天）的函数关系近似满足P（x）=1+$\frac{k}{x}$（k为正的常数），日销售量Q（x）（件）与时间x（天）的部分数据如表所示：
已知第2哦天的日销售量为126百元．
（Ⅰ）求k的值；
（Ⅱ）给出以下三种函数模型：
①Q（x）=a•bx；
②Q（x）=a•logbx；
③Q（x）=a|x-25|+b．
请您根据如表中的数据，从中选择你认为最合适的一种函数来描述日销售量Q（x）（件）与时间x（天）的变化关系，并求出该函数的解析式；
（Ⅲ）求该服装的日销收入f（x）（1≤x≤30，x∈N*）（百元）的最小值．
| x（天） | 10 | 20 | 25 | 30 |
| Q（x）（件） | 110 | 120 | 125 | 120 |
（Ⅰ）求k的值；
（Ⅱ）给出以下三种函数模型：
①Q（x）=a•bx；
②Q（x）=a•logbx；
③Q（x）=a|x-25|+b．
请您根据如表中的数据，从中选择你认为最合适的一种函数来描述日销售量Q（x）（件）与时间x（天）的变化关系，并求出该函数的解析式；
（Ⅲ）求该服装的日销收入f（x）（1≤x≤30，x∈N*）（百元）的最小值．
14．抛物线x2=ay（a∈R）的焦点坐标为（ ）
| A． | （$\frac{a}{2}$，0） | B． | （$\frac{a}{4}$，0） | C． | （0，$\frac{a}{2}$） | D． | （0，$\frac{a}{4}$） |
8．若函数f（x）=21n（x+1）-1nax在其定义域内有且只有一个零点，则实数a的取值集合为（ ）
| A． | |4| | B． | （-∞，4] | C． | （-∞，0） | D． | （-∞，0）∪{4} |
9．在△ABC中，若A=30°，a=2，b=2$\sqrt{3}$，则此三角形解的个数为（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 不能确定 |